Analysis for Quiz 12: Brain Power Enrichment Quiz (I)

Analysis for Quiz 12: Brain Power Enrichment Quiz (I)

Question 1: If $a\gt b$ and $c\gt d$ are true, then we can say $a+c\gt b+d$ is always true.

A. Correct.
B. Incorrect.

Answer:

Yes, that is always correct, regardless if $a,\,b,\,c,\,d$ are negative or positive real number.

Take for example, we have:

$-6\gt -8$ and $-10\gt -12$ are true, then we can say $-16\gt -20$ is true.

$0.2\gt 0.1$ and $0.05\gt 0.04$ are true, then we can say $0.25\gt 0.14$ is true.

$6\gt 3$ and $5\gt 4$ are true, then we can say $11\gt 7$ is true.

Therefore the answer is A.


Question 2: If $a\gt b$ and $c\gt d$are true, then we can say $a-c\gt b-d$ is always true.

A. Correct.
B. Incorrect.


Answer:
We must exercise cautious here, as if given $a\gt b$ and $c\gt d$are true, then we can say $a-c\gt b-d$ is not necessarily always true. I will show you one counter-example to defy the logic of it.

Take for example, we have:

$30\gt 20$ and $28\gt 16$ are true, then $(30-28=2)\gt (20-16=4)$ is NOT true albeit

$100\gt 98$ and $99\gt 98.5$ are true, then we can say $(100-99=1)\gt (98-98.5=0.5)$ is true.

It's enough to find one counter-example to refute the claim that $a-c\gt b-d$ is always true given $a\gt b$ and $c\gt d$.

Therefore, the answer for question 2 is B.

Question 3: If $a\gt b$ and $c\gt d$ are true, then we can say $ac\gt bd$ is always true.

A. Correct.
B. Incorrect.


Answer:

Similarly, the above inequality is NOT always true, given $a\gt b$ and $c\gt d$ are true. It's suffice to think of one counter example to prove it false.

Consider $-2\gt -3$ and $3\gt 1$, then $(-2)(3)=-6 \gt (-3)(1)=-3$ is pure wrong.

Therefore, the answer is B..

Question 4: Without the help of calculator, check the validity of the inequality $\sqrt{1000}-\sqrt{998} \gt \sqrt{998}-\sqrt{996}$.

A. Correct.
B. Incorrect.

Answer:

It's tempting to mark correct as the answer, if you have answered the question 2 wrongly because

$\sqrt{1000} \gt \sqrt{998}$ and $\sqrt{998} \gt \sqrt{996}$ so subtracting the second by the first will give the inequality as suggested as the question and therefore the answer is that that inequality is a correct statement.

But, little do you know the difference between $\sqrt{1000}-\sqrt{998}\approx 0.031638603$ is less than the difference between $\sqrt{998}-\sqrt{996}\approx 0.031670321$ and hence, $\sqrt{1000}-\sqrt{998} \lt \sqrt{998}-\sqrt{996}$.

Since the problem has mentioned the restriction of using calculator to see the differences between the LHS and RHS of the inequality, we could go back to the most original and traditional way to figure out the answer.

We square both sides of the inequality and see where that leads us:

$\sqrt{1000}-\sqrt{998} \gt \sqrt{998}-\sqrt{996}$

$\sqrt{1000}+\sqrt{996} \gt 2\sqrt{998}$

$(\sqrt{1000}+\sqrt{996})^2 \gt (2\sqrt{998})^2$

$1000+996+2\sqrt{1000}\sqrt{996} \gt 4(998)$

$2\sqrt{1000}\sqrt{996}  \gt 4(998)-1000-996$

$\sqrt{1000}\sqrt{996}  \gt 998$

$(\sqrt{1000}\sqrt{996})^2  \gt (998)^2$

$996000  \gt 996004$

We have reached to a contradiction and hence the given inequality is false and the answer is hence incorrect.

The diagram below represents the graph $y=x$ and the two right-angled triangles $ABC$ and $CDE$.

Question 5: Consider the two right-angled triangles $ABC$ and $CDE$ that share the same length, i.e. $L1=L2=1$ unit.
Compare $H1$ and $H2$.

A. $H1=H2.$
B. $H1\gt H2.$
B. $H1\lt H2.$

Answer:

Note that the two right-angled triangles $ABC$ and $CDE$ are congruent, therefore their heights must be the same.

Therefore A. $(H1=H2)$ is the answer.


The diagram below shows a curve and the two right-angled triangles ABC and CDE with the same lengths.

Question 6: Consider the two right-angled triangles $ABC$ and $CDE$ where $L1=L2=1$unit.
Compare $H1$ and $H2$.

A. $H1=H2.$
B. $H1\gt H2.$
B. $H1\lt H2.$


Answer:

The two right-angled triangles $ABC$ and $CDE$ have the same length where $L1=L2=1$unit, but the vertices of $A,\,C$ from triangle $ABC$ and $C,\,E$ from triangle $CDE$ lie on the concave up curve instead of a straight line $y=x$, in other words, as you move along the graph from left to right from $A$ to $C$ and then from $C$ to $E$, you notice the "hill (hypotenuse side of triangle)" becomes steeper.

Therefore, the height of triangle $CDE$, $H2$ is greater than the height of triangle $ABC$, $H1$.

This actually has everything to do with the behavior of the curve where the vertices $A,\,C$ from triangle $ABC$ and $C,\,E$ from triangle $CDE$ lie.

Therefore C is the answer.


Question 7: Which of the diagram below represents the graph of $y=\sqrt{x}$?

A.
B.
C.

Answer:

Regardless if we are teachers or students, we all have to be familiar with the graph of the function type $y=x^n$, given $n$ is a rational number $\dfrac{p}{q}$.

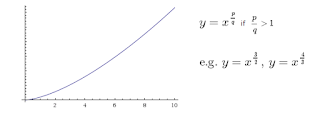
If $0\lt \dfrac{p}{q}\lt 1$, we have:

If $\dfrac{p}{q}\gt 1$, we have:

Therefore, B is the graph of $y=\sqrt{x}$.


Question 8: Reflect back on how you approached question 4, now, do you think you have acquired some knowledge to tell for certain if $\sqrt{1000}-\sqrt{998} \gt \sqrt{998}-\sqrt{996}$ or $\sqrt{1000}-\sqrt{998} \lt \sqrt{998}-\sqrt{996}$?

A. Yes.
B. No.

Answer:

Of course the answer is the absolute yes!!!

We know since the graph of $y=\sqrt{x}$ is in question, where we now have the right-angled triangles $ABC$ and $CDE$ with $A=(996,\,\sqrt{996})$, $C=(998,\,\sqrt{998})$ and $E=(1000,\,\sqrt{1000})$.

We note that the two triangles have the same length and since $y=\sqrt{x}$ is a concave down curve, therefore we must have the height of the triangle on the right is less than the height of the triangle on the left, and therefore, $\sqrt{1000}-\sqrt{998} \lt \sqrt{998}-\sqrt{996}$ is the correct inequality.


Question 9: Which one is greater?

$\text{A.}\,\,\,\sqrt[6]{2n+3}-\sqrt[6]{2n+1}$
$\text{B.}\,\,\,\sqrt[6]{2n+1}-\sqrt[6]{2n-1}$

Answer:

First, note that $2n+3-(2n+1)=2$ and $2n+1-(2n-1)=2$.

Second, if we have the graph of $y=\sqrt[6]{x}$, we know it's a concave down curve.

Now, says we construct the graph and create the two right-angled triangles $PQR$ and $RST$ where $P=(2n-1,\,\sqrt[6]{2n-1})$, $R=(2n+1,\,\sqrt[6]{2n+1})$ and $T=(2n+3,\,\sqrt[6]{2n+3})$ on the same coordinate plane, we know both right-angled triangles have the same length, and the height of the triangle on the right is surely less than the height of the triangle on the right, therefore, $\text{B.}\,\,\,\sqrt[6]{2n+1}-\sqrt[6]{2n-1}$ is greater.