Analysis Quiz 16: Multiple-Choice Math (Square Root Inequality)
Question 1: Which of the methods below do you think can be used to prove $\sqrt{3}-\sqrt{2}\gt \sqrt{4}-\sqrt{3}$?
A. AM-GM Inequality.
B. Jensen's Inequality.
C. Cauchy–Schwarz inequality.
D. Squaring both sides of the equation and squaring again to remove the square root to make numerical comparison.
A collection of intriguing competition level problems for secondary school students.
Prove $\small a(a-c)^2+b(b-c)^2\ge (a-c)(b-c)(a+b-c)$ for all real $a,\,b,\,c\ge 0$: Second Attempt
For reals $a,\,b,\,c\ge 0$, prove the inequality
$a(a-c)^2+b(b-c)^2\ge (a-c)(b-c)(a+b-c)$
and state when the equality holds.
$a(a-c)^2+b(b-c)^2\ge (a-c)(b-c)(a+b-c)$
and state when the equality holds.
Prove $a(a-c)^2+b(b-c)^2\ge (a-c)(b-c)(a+b-c)$ for all real $a,\,b,\,c\ge 0$: First Attempt
For reals $a,\,b,\,c\ge 0$, prove the inequality
$a(a-c)^2+b(b-c)^2\ge (a-c)(b-c)(a+b-c)$
and state when the equality holds.
$a(a-c)^2+b(b-c)^2\ge (a-c)(b-c)(a+b-c)$
and state when the equality holds.
Schur's inequality
I believe Schur's inequality might, perhaps, to the majority of the students that it's an inequality formula that students would not use much in their math problems.
But Schur's inequality is really a very magical and helpful inequality that if we are sufficiently familiarized with it for the special cases when $t=1$ and $t=2$, then we could use this "weapon" to tackle for lots of hard inequality IMO/competition problems.
But Schur's inequality is really a very magical and helpful inequality that if we are sufficiently familiarized with it for the special cases when $t=1$ and $t=2$, then we could use this "weapon" to tackle for lots of hard inequality IMO/competition problems.
Sophie Germain's Identity
I would wager not all of you know or sufficiently familiar with the identity as shown below:
$a^{4} + 4b^{4}=(a^2+2b^2+2ab)(a^2+2b^2-2ab)$
It's actually a famous identity and it has a fancy name as well...it is called the Sophie Germain's Identity.
As the name suggests, Sophie Germain's identity was first discovered by Sophie Germain.
$a^{4} + 4b^{4}=(a^2+2b^2+2ab)(a^2+2b^2-2ab)$
It's actually a famous identity and it has a fancy name as well...it is called the Sophie Germain's Identity.
As the name suggests, Sophie Germain's identity was first discovered by Sophie Germain.
IMO Inequality problem
For the positive real numbers $x,\,y$ and $z$ that satisfy $\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=3$, prove that
$\dfrac{1}{\sqrt{x^3+1}}+\dfrac{1}{\sqrt{y^3+1}}+\dfrac{1}{\sqrt{z^3+1}}\le \dfrac{3}{\sqrt{2}}$.
My solution:
$\dfrac{1}{\sqrt{x^3+1}}+\dfrac{1}{\sqrt{y^3+1}}+\dfrac{1}{\sqrt{z^3+1}}\le \dfrac{3}{\sqrt{2}}$.
My solution:
Probabiliy II: Who has the winning strategy?
Consider a polynomial
$$P(x)=a_0+a_1x+\cdots+a_{2011}x^{2011}+x^{2012}$$
Nigel and Jessica are playing the following game. In turn, they choose one of the coefficients $a_0,\,\cdots,\,a_{2011}$ and assign a real value to it. Nigel has the first move. Once a value is assigned to a coefficient, it cannot be changed any more. The game ends after all the coefficients have been assigned values.
$$P(x)=a_0+a_1x+\cdots+a_{2011}x^{2011}+x^{2012}$$
Nigel and Jessica are playing the following game. In turn, they choose one of the coefficients $a_0,\,\cdots,\,a_{2011}$ and assign a real value to it. Nigel has the first move. Once a value is assigned to a coefficient, it cannot be changed any more. The game ends after all the coefficients have been assigned values.
Find all pairs of integer solutions $x(y^2 + 9) + y(x^2 − 9) + x^2(x − 6) = 0$
My solution:
Before revealing my method of solving, I wish to tell you how I encountered students kept asking me why should they study quadratic function. How can they be useful.. They said quadratic functions have nothing special, and it's really easy peasy to find for its discriminant, and to completing the square to look for its optimal point and factoring it to investigate its roots.
Yes, that's all that to it for quadratic functions, but when you progress into higher grade, you would encounter problem like solving the equation for integer solutions.
That is when the concept of quadratic function creeps in to assist us in finding all possible integer solutions. How? Continue reading to figure out the answer.
Is there a real number $x$, that the expressions $\tan x + \sqrt{3}$ and $\cot x+ \sqrt{3}$ are both integers?
Is there a real number $x$, that the expressions $\tan x + \sqrt{3}$ and $\cot x+ \sqrt{3}$ are both integers?
My solution:
First, let's assume $\tan x + \sqrt{3}=a$ and $\cot x+ \sqrt{3}=b$ where $a,\,b$ are both integers.
My solution:
First, let's assume $\tan x + \sqrt{3}=a$ and $\cot x+ \sqrt{3}=b$ where $a,\,b$ are both integers.
Probabiliy: Who has the winning strategy?
Consider a polynomial
$$P(x)=a_0+a_1x+\cdots+a_{2011}x^{2011}+x^{2012}$$
Nigel and Jessica are playing the following game. In turn, they choose one of the coefficients $a_0,\,\cdots,\,a_{2011}$ and assign a real value to it. Nigel has the first move. Once a value is assigned to a coefficient, it cannot be changed any more. The game ends after all the coefficients have been assigned values.
$$P(x)=a_0+a_1x+\cdots+a_{2011}x^{2011}+x^{2012}$$
Nigel and Jessica are playing the following game. In turn, they choose one of the coefficients $a_0,\,\cdots,\,a_{2011}$ and assign a real value to it. Nigel has the first move. Once a value is assigned to a coefficient, it cannot be changed any more. The game ends after all the coefficients have been assigned values.
Third Solution: Find $k$ if $k\sin 6x=\sin 2x$ given $\dfrac{\cos 6x}{\cos 2x}=\dfrac{1}{6}$.
Find $k$ if $k\sin 6x=\sin 2x$ given $\dfrac{\cos 6x}{\cos 2x}=\dfrac{1}{6}$.
Third method:
Second Method: Find $k$ if $k\sin 6x=\sin 2x$ given $6\cos 6x=\cos 2x$.
Find $k$ if $k\sin 6x=\sin 2x$ given $\dfrac{\cos 6x}{\cos 2x}=\dfrac{1}{6}$.
Second method:
Note that we can rewrite the given equality $6\cos 6x=\cos 2x$ as $\dfrac{\cos 6x}{\cos 2x}=\dfrac{1}{6}$, also, our target expression as $\dfrac{\sin 6x}{\sin 2x}=\dfrac{1}{k}$.
Second method:
Note that we can rewrite the given equality $6\cos 6x=\cos 2x$ as $\dfrac{\cos 6x}{\cos 2x}=\dfrac{1}{6}$, also, our target expression as $\dfrac{\sin 6x}{\sin 2x}=\dfrac{1}{k}$.
Find $k$ if $k\sin 6x=\sin 2x$ given $6\cos 6x=\cos 2x$.
Find $k$ if $k\sin 6x=\sin 2x$ given $\dfrac{\cos 6x}{\cos 2x}=\dfrac{1}{6}$.
There are at least three different methods of solving for this particular problem. One is rather straightforward, and the other two methods are quite special.
There are at least three different methods of solving for this particular problem. One is rather straightforward, and the other two methods are quite special.
Floor function system
Solve the following equation in the real number system:
$\left\lfloor{\log_2 x}\right\rfloor+\left\lfloor{\log_4 x}\right\rfloor=3$
$\left\lfloor{\log_2 x}\right\rfloor+\left\lfloor{\log_4 x}\right\rfloor=3$
Olympiad Math Problem: Find the maximum and minimum of P (Heuristic Solution)
Find the minimum and maximum of $P=\dfrac{y−x}{x+8y}$ for all real $x$ and $y$ that satisfy the equation $y^2(6-x^2)-xy-1=0$.
My solution:
Note that the given equality $y^2(6-x^2)-xy-1=0$ has the terms $y^2,\,x^2y^2$ and $xy$ while the target expression, $P$ is a rational function with the terms $x$ and $y$.
My solution:
Note that the given equality $y^2(6-x^2)-xy-1=0$ has the terms $y^2,\,x^2y^2$ and $xy$ while the target expression, $P$ is a rational function with the terms $x$ and $y$.
Prove the equality : $\sqrt{33 − 16\sqrt{3}\sin80^\circ}= 1+8\sin10^\circ$
Prove the equality :
$\sqrt{33 − 16\sqrt{3}\sin80^\circ}= 1+8\sin10^\circ$
First, note that
$\begin{align*}\cos^2 20^\circ&=\cos20^\circ(2\cdot\dfrac{1}{2}\cos20^\circ)\\&=\cos20^\circ(2\cos60^\circ\cos20^\circ)\\&=\cos20^\circ((\cos(60^\circ+20^\circ)+\cos(60^\circ-20^\circ))\\&=\cos20^\circ(\cos80^\circ+\cos40^\circ)\\&=\cos20^\circ\cos80^\circ+\cos20^\circ\cos40^\circ\\&=\dfrac{1}{2}(\cos(20^\circ+80^\circ)+\cos(80^\circ-20^\circ))+\dfrac{1}{2}(\cos(20^\circ+40^\circ)+\cos(40^\circ-20^\circ))\\&=\dfrac{1}{2}(\cos100^\circ+\cos60^\circ)+\dfrac{1}{2}(\cos60^\circ+\cos20^\circ)\\&=\dfrac{1}{2}\left(\cos(90^\circ+10^\circ)+\dfrac{1}{2}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}+\cos 20^\circ\right)\\&=\dfrac{1}{2}(-\sin 10^\circ)+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{2}\cos 20^\circ\\&=\dfrac{1}{2}(\cos20^\circ-\sin10^\circ+1)\end{align*}$
$\sqrt{33 − 16\sqrt{3}\sin80^\circ}= 1+8\sin10^\circ$
First, note that
$\begin{align*}\cos^2 20^\circ&=\cos20^\circ(2\cdot\dfrac{1}{2}\cos20^\circ)\\&=\cos20^\circ(2\cos60^\circ\cos20^\circ)\\&=\cos20^\circ((\cos(60^\circ+20^\circ)+\cos(60^\circ-20^\circ))\\&=\cos20^\circ(\cos80^\circ+\cos40^\circ)\\&=\cos20^\circ\cos80^\circ+\cos20^\circ\cos40^\circ\\&=\dfrac{1}{2}(\cos(20^\circ+80^\circ)+\cos(80^\circ-20^\circ))+\dfrac{1}{2}(\cos(20^\circ+40^\circ)+\cos(40^\circ-20^\circ))\\&=\dfrac{1}{2}(\cos100^\circ+\cos60^\circ)+\dfrac{1}{2}(\cos60^\circ+\cos20^\circ)\\&=\dfrac{1}{2}\left(\cos(90^\circ+10^\circ)+\dfrac{1}{2}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}+\cos 20^\circ\right)\\&=\dfrac{1}{2}(-\sin 10^\circ)+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{2}\cos 20^\circ\\&=\dfrac{1}{2}(\cos20^\circ-\sin10^\circ+1)\end{align*}$
Olympiad Math Problem: Find the maximum and minimum of P (First Attempt)
Find the minimum and maximum of $P=\dfrac{y−x}{x+8y}$ for all real $x$ and $y$ that satisfy the equation $y^2(6-x^2)-xy-1=0$.
On one hand, this is not a unmanageable Olympiad Mathematics optimization problem, on the other hand, this problem allows us to show students how powerful algebraic manipulation is when we use it diligently and how effective the accurate solution we could have arrived compared to all the alternatives.
On one hand, this is not a unmanageable Olympiad Mathematics optimization problem, on the other hand, this problem allows us to show students how powerful algebraic manipulation is when we use it diligently and how effective the accurate solution we could have arrived compared to all the alternatives.
Heuristic Solution: Determine the product of $q(r_1)\cdot q(r_2)\cdot q(r_3)\cdot q(r_4)\cdot q(r_5)$.
Given $p(x)=x^5+x^2+1$ have roots $r_1,\,r_2,\,r_3,\,r_4,\,r_5$. Let $q(x)=x^2-2$. Determine the product of $q(r_1)\cdot q(r_2)\cdot q(r_3)\cdot q(r_4)\cdot q(r_5)$.
Determine the product of $q(r_1)\cdot q(r_2)\cdot q(r_3)\cdot q(r_4)\cdot q(r_5)$.
Given $p(x)=x^5+x^2+1$ have roots $r_1,\,r_2,\,r_3,\,r_4,\,r_5$. Let $q(x)=x^2-2$. Determine the product of $q(r_1)\cdot q(r_2)\cdot q(r_3)\cdot q(r_4)\cdot q(r_5)$.
If we attempt at the problem using the Vieta's formulas, then we might have to work a bit harder and longer to determine the value of the required product. But, it is a workable approach and let's see how and what procedures are needed in order to reach to the final result.
From the polynomial of $p(x)=x^5-0x^4+0x^3-(-1)x^2+0x-(-1)$, we have:
$r_1+r_2+r_3+r_4+r_5=0$
$r_1r_2+r_1r_3+r_1r_4+r_1r_5+r_2r_3+r_2r_4+r_2r_5+r_3r_4+r_3r_5+r_4r_5=0$
$r_1r_2r_3+r_1r_2r_4+r_1r_2r_5+r_1r_3r_4+r_1r_3r_5+r_1r_4r_5+r_2r_3r_4+r_2r_3r_5+r_2r_4r_5+r_3r_4r_5=-1$
$r_1r_2r_3r_4+r_1r_2r_3r_5+r_1r_2r_4r_5+r_1r_3r_4r_5+r_2r_3r_4r_5=0$
$r_1r_2r_3r_4r_5=-1$
Our target expression is $(r_1-2)(r_2-2)(r_3-2)(r_4-2)(r_5-2)$, which upon expanding we have:
$(r_1-2)(r_2-2)(r_3-2)(r_4-2)(r_5-2)$
$=(r_1r_2r_3r_4r_5)^2+2(r_1^2r_2^2r_3^2r_4^2+r_1^2r_2^2r_3^2r_5^2+r_1^2r_2^2r_4^2r_5^2+r_1^2r_3^2r_4^2r_5^2+r_2^2r_3^2r_4^2r_5^2)$
$\,\,\,\,\,\,+4(r_1^2r_2^2r_3^2+r_1^2r_2^2r_4^2+r_1^2r_2^2r_5^2+r_1^2r_3^2r_4^2+r_1^2r_3^2r_5^2+r_1^2r_4^2r_5^2+r_2^2r_3^2r_4^2+r_2^2r_3^2r_5^2+r_2^2r_4^2r_5^2+r_3^2r_4^2r_5^2)$
$\,\,\,\,\,+8(r_1^2r_2^2+r_1^2r_3^2+r_1^2r_4^2+r_1^2r_5^2+r_2^2r_3^2+r_2^2r_4^2+r_2^2r_5^2+r_3^2r_4^2+r_3^2r_5^2+r_4^2r_5^2)$
$\,\,\,\,\,+16(r_1^2+r_2^2+r_3^2+r_4^2+r_5^2)+32$
But we know too:
$(r_1+r_2+r_3+r_4+r_5)^2$
$=r_1^2+r_2^2+r_3^2+r_4^2+r_5^2+2(r_1r_2+r_1r_3+r_1r_4+r_1r_5+r_2r_3+r_2r_4+r_2r_5+r_3r_4+r_3r_5+r_4r_5)$
This implies $0=r_1^2+r_2^2+r_3^2+r_4^2+r_5^2+2(0)$, i.e.
[MATH]\color{yellow}\bbox[5px,purple]{r_1^2+r_2^2+r_3^2+r_4^2+r_5^2=0}[/MATH]
$(r_1^2+r_2^2+r_3^2+r_4^2+r_5^2)^2$
$=r_1^4+r_2^4+r_3^4+r_4^4+r_5^4+2(r_1^2r_2^2+r_1^2r_3^2+r_1^2r_4^2+r_1^2r_5^2+r_2^2r_3^2+r_2^2r_4^2+r_2^2r_5^2+r_3^2r_4^2+r_3^2r_5^2+r_4^2r_5^2)$
$0=r_1^4+r_2^4+r_3^4+r_4^4+r_5^4+2(r_1^2r_2^2+r_1^2r_3^2+r_1^2r_4^2+r_1^2r_5^2+r_2^2r_3^2+r_2^2r_4^2+r_2^2r_5^2+r_3^2r_4^2+r_3^2r_5^2+r_4^2r_5^2)$
$-4(r_1^4+r_2^4+r_3^4+r_4^4+r_5^4)=8(r_1^2r_2^2+r_1^2r_3^2+r_1^2r_4^2+r_1^2r_5^2+r_2^2r_3^2+r_2^2r_4^2+r_2^2r_5^2+r_3^2r_4^2+r_3^2r_5^2+r_4^2r_5^2)$
Ah, I just don't have the motivation to keep going with this most likely the fruitless approach, as it will be testing my patient to the limit to look for the appropriate expression or values for:
$r_1^2r_2^2r_3^2r_4^2+r_1^2r_2^2r_3^2r_5^2+r_1^2r_2^2r_4^2r_5^2+r_1^2r_3^2r_4^2r_5^2+r_2^2r_3^2r_4^2r_5^2$ and
$r_1^2r_2^2r_3^2+r_1^2r_2^2r_4^2+r_1^2r_2^2r_5^2+r_1^2r_3^2r_4^2+r_1^2r_3^2r_5^2+r_1^2r_4^2r_5^2+r_2^2r_3^2r_4^2+r_2^2r_3^2r_5^2+r_2^2r_4^2r_5^2+r_3^2r_4^2r_5^2$
It's high time to wise up to stop with this unproductive approach and think for alternative.
I will show you the solution provided by my dearest math mentor from the U.K. in my next blog post, in the mean time, I hope you could make the best of this opportunity to attempt at the solution, who knows, perhaps you could come up with the heuristic solution? :D
If we attempt at the problem using the Vieta's formulas, then we might have to work a bit harder and longer to determine the value of the required product. But, it is a workable approach and let's see how and what procedures are needed in order to reach to the final result.
From the polynomial of $p(x)=x^5-0x^4+0x^3-(-1)x^2+0x-(-1)$, we have:
$r_1+r_2+r_3+r_4+r_5=0$
$r_1r_2+r_1r_3+r_1r_4+r_1r_5+r_2r_3+r_2r_4+r_2r_5+r_3r_4+r_3r_5+r_4r_5=0$
$r_1r_2r_3+r_1r_2r_4+r_1r_2r_5+r_1r_3r_4+r_1r_3r_5+r_1r_4r_5+r_2r_3r_4+r_2r_3r_5+r_2r_4r_5+r_3r_4r_5=-1$
$r_1r_2r_3r_4+r_1r_2r_3r_5+r_1r_2r_4r_5+r_1r_3r_4r_5+r_2r_3r_4r_5=0$
$r_1r_2r_3r_4r_5=-1$
Our target expression is $(r_1-2)(r_2-2)(r_3-2)(r_4-2)(r_5-2)$, which upon expanding we have:
$(r_1-2)(r_2-2)(r_3-2)(r_4-2)(r_5-2)$
$=(r_1r_2r_3r_4r_5)^2+2(r_1^2r_2^2r_3^2r_4^2+r_1^2r_2^2r_3^2r_5^2+r_1^2r_2^2r_4^2r_5^2+r_1^2r_3^2r_4^2r_5^2+r_2^2r_3^2r_4^2r_5^2)$
$\,\,\,\,\,\,+4(r_1^2r_2^2r_3^2+r_1^2r_2^2r_4^2+r_1^2r_2^2r_5^2+r_1^2r_3^2r_4^2+r_1^2r_3^2r_5^2+r_1^2r_4^2r_5^2+r_2^2r_3^2r_4^2+r_2^2r_3^2r_5^2+r_2^2r_4^2r_5^2+r_3^2r_4^2r_5^2)$
$\,\,\,\,\,+8(r_1^2r_2^2+r_1^2r_3^2+r_1^2r_4^2+r_1^2r_5^2+r_2^2r_3^2+r_2^2r_4^2+r_2^2r_5^2+r_3^2r_4^2+r_3^2r_5^2+r_4^2r_5^2)$
$\,\,\,\,\,+16(r_1^2+r_2^2+r_3^2+r_4^2+r_5^2)+32$
But we know too:
$(r_1+r_2+r_3+r_4+r_5)^2$
$=r_1^2+r_2^2+r_3^2+r_4^2+r_5^2+2(r_1r_2+r_1r_3+r_1r_4+r_1r_5+r_2r_3+r_2r_4+r_2r_5+r_3r_4+r_3r_5+r_4r_5)$
This implies $0=r_1^2+r_2^2+r_3^2+r_4^2+r_5^2+2(0)$, i.e.
[MATH]\color{yellow}\bbox[5px,purple]{r_1^2+r_2^2+r_3^2+r_4^2+r_5^2=0}[/MATH]
$(r_1^2+r_2^2+r_3^2+r_4^2+r_5^2)^2$
$=r_1^4+r_2^4+r_3^4+r_4^4+r_5^4+2(r_1^2r_2^2+r_1^2r_3^2+r_1^2r_4^2+r_1^2r_5^2+r_2^2r_3^2+r_2^2r_4^2+r_2^2r_5^2+r_3^2r_4^2+r_3^2r_5^2+r_4^2r_5^2)$
$0=r_1^4+r_2^4+r_3^4+r_4^4+r_5^4+2(r_1^2r_2^2+r_1^2r_3^2+r_1^2r_4^2+r_1^2r_5^2+r_2^2r_3^2+r_2^2r_4^2+r_2^2r_5^2+r_3^2r_4^2+r_3^2r_5^2+r_4^2r_5^2)$
$-4(r_1^4+r_2^4+r_3^4+r_4^4+r_5^4)=8(r_1^2r_2^2+r_1^2r_3^2+r_1^2r_4^2+r_1^2r_5^2+r_2^2r_3^2+r_2^2r_4^2+r_2^2r_5^2+r_3^2r_4^2+r_3^2r_5^2+r_4^2r_5^2)$
Ah, I just don't have the motivation to keep going with this most likely the fruitless approach, as it will be testing my patient to the limit to look for the appropriate expression or values for:
$r_1^2r_2^2r_3^2r_4^2+r_1^2r_2^2r_3^2r_5^2+r_1^2r_2^2r_4^2r_5^2+r_1^2r_3^2r_4^2r_5^2+r_2^2r_3^2r_4^2r_5^2$ and
$r_1^2r_2^2r_3^2+r_1^2r_2^2r_4^2+r_1^2r_2^2r_5^2+r_1^2r_3^2r_4^2+r_1^2r_3^2r_5^2+r_1^2r_4^2r_5^2+r_2^2r_3^2r_4^2+r_2^2r_3^2r_5^2+r_2^2r_4^2r_5^2+r_3^2r_4^2r_5^2$
It's high time to wise up to stop with this unproductive approach and think for alternative.
I will show you the solution provided by my dearest math mentor from the U.K. in my next blog post, in the mean time, I hope you could make the best of this opportunity to attempt at the solution, who knows, perhaps you could come up with the heuristic solution? :D
Factorize $x^5+x^4+1$
Factorize $x^5+x^4+1$.
If you have never come across this problem before, I'll bet you dollars to donuts you might reply resolutely that $x^5+x^4+1$ could not be factorized. :D
But, fact is, it can. And one doesn't have to have a crystal ball to "see" the factors of $x^5+x^4+1$. We can work it out, slowly but surely!
If you have never come across this problem before, I'll bet you dollars to donuts you might reply resolutely that $x^5+x^4+1$ could not be factorized. :D
But, fact is, it can. And one doesn't have to have a crystal ball to "see" the factors of $x^5+x^4+1$. We can work it out, slowly but surely!
Learn To Think Mathematically
Train new mode of thinking and hence deduce something useful as problem solving trick.
It's a breeze if you're asked to factor
$a^2-b^2$
since it's obviously a difference of square that factored as $a^2-b^2=(a+b)(a-b)$.
It's a breeze if you're asked to factor
$a^2-b^2$
since it's obviously a difference of square that factored as $a^2-b^2=(a+b)(a-b)$.
How Learning Patterns Leads to Brighter Students?
Do you know we could make optimal use of the things that we have been told they exist since we were primary school students such as the table that contains the very common info, like the table of squares?
$x$ $x^2$
$1$ $1$
$2$ $4$
$3$ $9$
$4$ $16$
$x$ $x^2$
$1$ $1$
$2$ $4$
$3$ $9$
$4$ $16$
Find the positive integer numbers $a$ and $b$ such that $65(a^3b^3 + a^2 + b^2) = 81(ab^3 + 1)$.
Find the positive integer numbers $a$ and $b$ such that $65(a^3b^3 + a^2 + b^2) = 81(ab^3 + 1)$.
It's highly unlikely that there is a way to factor $65(a^3b^3+a^2+b^2)-81(ab^3+1)=0$ and when we're asked to solve for the positive integer solutions, we would always think of treating the given equation as a quadratic function and then set its discriminant greater than or equal to zero, but this can't be the case here:
It's highly unlikely that there is a way to factor $65(a^3b^3+a^2+b^2)-81(ab^3+1)=0$ and when we're asked to solve for the positive integer solutions, we would always think of treating the given equation as a quadratic function and then set its discriminant greater than or equal to zero, but this can't be the case here:
IMO Algebra Problem: Find maximum of a₁+a₂+a₃+a₄-a₁a₂-a₁a₃-a₁a₄-a₂a₃-a₂a₄-a₃a₄+a₁a₂a₃+a₁a₂a₄+a₁a₃a₄+a₂a₃a₄-a₁a₂a₃a₄
Find the maximum of
$a_1+a_2+a_3+a_4-a_1a_2-a_1a_3-a_1a_4-a_2a_3-a_2a_4-a_3a_4+a_1a_2a_3+a_1a_2a_4+a_1a_3a_4+a_2a_3a_4-a_1a_2a_3a_4$
where $|a_i|\le 1,\,i=1,\,2,\,3,\,4$.
$a_1+a_2+a_3+a_4-a_1a_2-a_1a_3-a_1a_4-a_2a_3-a_2a_4-a_3a_4+a_1a_2a_3+a_1a_2a_4+a_1a_3a_4+a_2a_3a_4-a_1a_2a_3a_4$
where $|a_i|\le 1,\,i=1,\,2,\,3,\,4$.
Blaise Pascal: Little Of Everything
It's very important to know a little of everything, as it could help us to become one of the most stand out competitors who has the most competitive edge and that we cannot be replaced easily by anyone else.
Sound too good to be true? It turns out it was. :D
Sound too good to be true? It turns out it was. :D
Simplify $2(x^8+y^8+z^8)-(x^4+y^4+z^4)^2$ (First Attempt)
Simplify $2(x^8+y^8+z^8)-(x^4+y^4+z^4)^2$.
Please don't be tempted by the temptation to expand the second term as it will lead to headache and no closer to the answer of the more simplified form:
Please don't be tempted by the temptation to expand the second term as it will lead to headache and no closer to the answer of the more simplified form:
Prove $\large 1000!^{\frac{1}{1000}}>999!^{\frac{1}{999}}$.
Prove $\large 1000!^{\frac{1}{1000}}>999!^{\frac{1}{999}}$.
This inequality would be easy to prove if one uses the more advance knowledge, like Stirling's formula where it states when $n\rightarrow \infty$ then we have $n!\approx \dfrac{n^n}{e^n}\sqrt{2\pi n}$.
But, elementary method works well too in this problem.
This inequality would be easy to prove if one uses the more advance knowledge, like Stirling's formula where it states when $n\rightarrow \infty$ then we have $n!\approx \dfrac{n^n}{e^n}\sqrt{2\pi n}$.
But, elementary method works well too in this problem.
Hard Inequality Problem
Let $x,\,y,\,z$ be real numbers such that $6x+2y+3z=12+xyz$.
Prove that $(x^2+1)(y^2+9)(z^2+4)\ge 144$.
Note that
$(x^2+1)(y^2+9)(z^2+4)-(6x+2y+3z-xyz)^2$
Prove that $(x^2+1)(y^2+9)(z^2+4)\ge 144$.
Note that
$(x^2+1)(y^2+9)(z^2+4)-(6x+2y+3z-xyz)^2$
Prove that: ⌊√(n)+√(n+1)⌋=⌊√(4n+2)⌋, for all positive integer n.
Prove that: $\left\lfloor{\sqrt{n}+\sqrt{n+1}}\right\rfloor= \left\lfloor{\sqrt{4n+2}}\right\rfloor$, for all $n\in N$.
My solution:
Step 1:
Note that:
$4n^2+4n\lt 4n^2+4n+1\lt 4n^2+8n+4$
My solution:
Step 1:
Note that:
$4n^2+4n\lt 4n^2+4n+1\lt 4n^2+8n+4$
Prove that: $⌊√n+1/(√n+√(n+2))⌋=⌊√n⌋$, for all $n\in N$.
Prove that: $\left\lfloor{\sqrt{n}+\dfrac{1}{\sqrt{n}+\sqrt{n+2}}}\right\rfloor= \left\lfloor{\sqrt{n}}\right\rfloor$, for all $n\in N$.
My solution:
Step 1:
First, note that the expression inside the floor function on the left can be rewritten such that we have:
My solution:
Step 1:
First, note that the expression inside the floor function on the left can be rewritten such that we have:
Without the help of calculator, evaluate $\sqrt[8]{10828567056280801}$.
Without the help of calculator, evaluate $\sqrt[8]{10828567056280801}$.
This might look like there will be a lot of guessing before getting the right answer. But, if you toy around with the figure $10828567056280801$, it's not hard to see we could rewrite it so that we have:
$10828567056280801$
This might look like there will be a lot of guessing before getting the right answer. But, if you toy around with the figure $10828567056280801$, it's not hard to see we could rewrite it so that we have:
$10828567056280801$
Prove $\sqrt{2}+\sqrt{3}\gt \pi$
Prove $\sqrt{2}+\sqrt{3}\gt \pi$.
Note that we could use the previously established result from the famous people or even our own finding to construct for the future conjectures and hence argument to help us in determining the plot that we are going to use to solve the new problem at hand, that is one of the very good traits of highly proficient problem solver.
Note that we could use the previously established result from the famous people or even our own finding to construct for the future conjectures and hence argument to help us in determining the plot that we are going to use to solve the new problem at hand, that is one of the very good traits of highly proficient problem solver.
Classic proof: $\dfrac{22}{7}\gt \pi$
Prove $\dfrac{22}{7}\gt \pi$.
There is a very classic and elegant proof for this inequality involving $\pi$ and its fraction representative $\dfrac{22}{7}$.
It's using the graphical and integration method to prove $\dfrac{22}{7}\gt \pi$.
There is a very classic and elegant proof for this inequality involving $\pi$ and its fraction representative $\dfrac{22}{7}$.
It's using the graphical and integration method to prove $\dfrac{22}{7}\gt \pi$.
Develep the power of observation
If you're given the two graphs that are plotted in the same Cartesian plane below, what do you notice?
Analysis Quiz 14: Challenging Mathematics Drill Quiz
$\log_2 (3)+\log_6 (8)$
A. Their sum is less than zero.
B. Their sum is greater than zero.
Answer:
In order to answer the question correctly, we must be super familiar with how the graph of $y=\log_{10} x$ behaves.
How to improve your thinking skills? (III)
Prove $\dfrac{\pi}{4}+\dfrac{1}{6}\gt \arctan\left({\dfrac{6}{5}}\right)$.
Do you know if we're pretty familiar with how the graph of a particular function behaves on certain interval, we could set up a definite integral to prove some of the inequality problems (be them hard, moderately hard or very difficult)?
Do you know if we're pretty familiar with how the graph of a particular function behaves on certain interval, we could set up a definite integral to prove some of the inequality problems (be them hard, moderately hard or very difficult)?
How to improve your thinking skills? (II)
Prove $\dfrac{\pi}{4}+\dfrac{1}{6}\gt \arctan\left({\dfrac{6}{5}}\right)$.
Let's pick up where we left off...we needed to complete the proof using the readily available formula that says
$\arctan\left({\dfrac{6}{5}}\right)=\dfrac{\pi}{4}+\dfrac{1}{10}-\dfrac{1}{100}+\dfrac{1}{1500}-\dfrac{1}{125000}+\dfrac{1}{750000}-\dfrac{1}{8750000}+\cdots$
such that we get
Let's pick up where we left off...we needed to complete the proof using the readily available formula that says
$\arctan\left({\dfrac{6}{5}}\right)=\dfrac{\pi}{4}+\dfrac{1}{10}-\dfrac{1}{100}+\dfrac{1}{1500}-\dfrac{1}{125000}+\dfrac{1}{750000}-\dfrac{1}{8750000}+\cdots$
such that we get
How to improve your thinking skills?
What methods one could use to prove inequalities IMO problems?
Off the top of your head, you might want to shout out that AM-GM inequality, Cauchy Schwarz inequality. Jensen's inequality are among the "hot" and popular methods that you would consider using to effectively prove the inequality hard IMO problem.
Off the top of your head, you might want to shout out that AM-GM inequality, Cauchy Schwarz inequality. Jensen's inequality are among the "hot" and popular methods that you would consider using to effectively prove the inequality hard IMO problem.
Prove that $x^7-2x^5+10x^2-1$ has no root greater than 1 (Heuristic Method)
Prove that $x^7-2x^5+10x^2-1$ has no root greater than 1.
Heuristic method:
The trick is to substitute $y+1$ for $x$ in the given function:
If $f(x)=x^7-2x^5+10x^2-1$, then after the substitution we see that we have:
Heuristic method:
The trick is to substitute $y+1$ for $x$ in the given function:
If $f(x)=x^7-2x^5+10x^2-1$, then after the substitution we see that we have:
Prove that $x^7-2x^5+10x^2-1$ has no root greater than 1 (Second post)
Prove that $x^7-2x^5+10x^2-1$ has no root greater than 1.
In the previous blog post, I mentioned of solving the equation $x^7-2x^5+10x^2-1=0$ so to show that the function $x^7-2x^5+10x^2-1$ has no root greater than 1.
But, that is a really bad idea. The reason why the question setters stated the problem so mostly because they wanted to avoid us to solve for the problem. To solve for the polynomial of degree seven is really difficult, plus, the polynomial couldn't be factorized and so the real roots are kind of "ugly", there are no exact values for them.
In the previous blog post, I mentioned of solving the equation $x^7-2x^5+10x^2-1=0$ so to show that the function $x^7-2x^5+10x^2-1$ has no root greater than 1.
But, that is a really bad idea. The reason why the question setters stated the problem so mostly because they wanted to avoid us to solve for the problem. To solve for the polynomial of degree seven is really difficult, plus, the polynomial couldn't be factorized and so the real roots are kind of "ugly", there are no exact values for them.
Prove that $x^7-2x^5+10x^2-1$ has no root greater than 1 (First Post)
Prove that $x^7-2x^5+10x^2-1$ has no root greater than 1.
This is one thought provoking problem, as it presents the golden opportunity for one to think hard and long so they understand the problem more well and that eventually will improve one's reasoning skill.
This is one thought provoking problem, as it presents the golden opportunity for one to think hard and long so they understand the problem more well and that eventually will improve one's reasoning skill.
(Heuristic Solution) Prove $35\sqrt{55}+55\sqrt{77}+77\sqrt{35}+35\sqrt{77}+55\sqrt{35}+77\sqrt{55}\gt 2310$.
Prove $35\sqrt{55}+55\sqrt{77}+77\sqrt{35}+35\sqrt{77}+55\sqrt{35}+77\sqrt{55}\gt 2310$.
My solution:
Note that we could rewrite the given LHS of the inequality as follows:
$35\sqrt{55}+55\sqrt{77}+77\sqrt{35}+35\sqrt{77}+55\sqrt{35}+77\sqrt{55}$
My solution:
Note that we could rewrite the given LHS of the inequality as follows:
$35\sqrt{55}+55\sqrt{77}+77\sqrt{35}+35\sqrt{77}+55\sqrt{35}+77\sqrt{55}$
Prove $35√55+55√77+77√35+35√77+55√35+77√55\gt 2310$.
Prove $35\sqrt{55}+55\sqrt{77}+77\sqrt{35}+35\sqrt{77}+55\sqrt{35}+77\sqrt{55}\gt 2310$.
The first idea that might sprang to your mind whenever you see square root terms and the inequality is you want to squaring both sides of the inequality and you are expected to finally prove a figure is larger than another figure and you are hence done.
The first idea that might sprang to your mind whenever you see square root terms and the inequality is you want to squaring both sides of the inequality and you are expected to finally prove a figure is larger than another figure and you are hence done.
For $a\gt b\gt 0$, prove that $\dfrac{a+b}{2}\gt \dfrac{a-b}{\ln a-\ln b}$.
For $a\gt b\gt 0$, prove that $\dfrac{a+b}{2}\gt \dfrac{a-b}{\ln a-\ln b}$.
There sure is many way to prove this problem, but I am going to show you one graphical method that if we recognize some function is always greater than the other in certain interval, then it makes the problem all that easier for us to crack.
There sure is many way to prove this problem, but I am going to show you one graphical method that if we recognize some function is always greater than the other in certain interval, then it makes the problem all that easier for us to crack.
Evaluate a+2b.
Suppose that there exist two positive real numbers $a$ and $b$ such that $(a-2) (a^2+2a-18)+ab(2a+b+18)-96+2(b-2)(b+3)(b+2)=0$.
Evaluate $a+2b$.
My solution:
Evaluate $a+2b$.
My solution:
Find the sum of all possible $a^3$, where $a$ is a rational figure (Heuristic Solution)
Given that $a$ is rational and the equation $ax^2+(a+2)x+a-1=0$ has integer roots.
Find the sum of all possible $a^3$.
It is very important for me to say out loud here that this solution is provided by my math friend, a retired math professor from the U.K.
Find the sum of all possible $a^3$.
It is very important for me to say out loud here that this solution is provided by my math friend, a retired math professor from the U.K.
Find the sum of all possible $a^3$, where $a$ is a rational figure.
Given that $a$ is rational and the equation $ax^2+(a+2)x+a-1=0$ has integer roots.
Find the sum of all possible $a^3$.
The solution will require deep and strategic thought but that doesn't mean this problem is impossible to solve.
If you know and are familiar with the manipulation trick that we could play on the rational number, we can see the solution pretty clearly.
Find the sum of all possible $a^3$.
The solution will require deep and strategic thought but that doesn't mean this problem is impossible to solve.
If you know and are familiar with the manipulation trick that we could play on the rational number, we can see the solution pretty clearly.
Analysis Quiz 13: Brain Power Enrichment Quiz (II)
Quiz 13: Brain Power Enrichment Quiz (II)
The diagram below represents the graph y=x and the coordinate points (2, 2), (4, 4) and (6, 6).
The diagram below represents the graph y=x and the coordinate points (2, 2), (4, 4) and (6, 6).
Expand Students' Horizon of Thinking
I have heard some very wise saying, it says "What we know isn’t what we need to know. Familiarity, process, and our comfort zones are only holding us back."
Too much familiarity is really bad for creativity. Too much experiences with the common problem may narrow down the choices that you have to deal with the problem at hand, you stick to the old ways of solving problems and you are unable to produce new ideas.
Too much familiarity is really bad for creativity. Too much experiences with the common problem may narrow down the choices that you have to deal with the problem at hand, you stick to the old ways of solving problems and you are unable to produce new ideas.
IMO Solving System Of Equation Problem (Heuristic Solution)
Solve the following system of equations in real $a,\,b,\,c,\,d$:
$a+b=9$
$ab+c+d=29$
$ad+bc=39$
$cd=18$
Heuristic solution:
$a+b=9$
$ab+c+d=29$
$ad+bc=39$
$cd=18$
Heuristic solution:
IMO Solving System Of Equation Problem (Second Attempt)
Solve the following system of equations in real $a,\,b,\,c,\,d$:
$a+b=9$
$ab+c+d=29$
$ad+bc=39$
$cd=18$
Previously we tried the elimination route and we failed.
$a+b=9$
$ab+c+d=29$
$ad+bc=39$
$cd=18$
Previously we tried the elimination route and we failed.
IMO Solving System Of Equation Problem (First Attempt)
Solve the following system of equations in real $a,\,b,\,c,\,d$:
$a+b=9$
$ab+c+d=29$
$ad+bc=39$
$cd=18$
$a+b=9$
$ab+c+d=29$
$ad+bc=39$
$cd=18$
Find all positive integers [MATH]n[/MATH] for which [MATH]\sqrt{n+\sqrt{1996}}[/MATH] exceeds [MATH]\sqrt{n-1}[/MATH] by an integer. (First Solution)
Find all positive integers [MATH]n[/MATH] for which [MATH]\sqrt{n+\sqrt{1996}}[/MATH] exceeds [MATH]\sqrt{n-1}[/MATH] by an integer.
My solution:
Let [MATH]\sqrt{n+\sqrt{1996}}-\sqrt{n-1}=k[/MATH], where [MATH]k[/MATH] is a positive integer.
[MATH]\sqrt{n+\sqrt{1996}}=k+\sqrt{n-1}[/MATH]
My solution:
Let [MATH]\sqrt{n+\sqrt{1996}}-\sqrt{n-1}=k[/MATH], where [MATH]k[/MATH] is a positive integer.
[MATH]\sqrt{n+\sqrt{1996}}=k+\sqrt{n-1}[/MATH]
IMO Integration Problem: Evaluate $\displaystyle\int^{\dfrac{\pi}{4}}_0 \dfrac{x}{(\sin x+\cos x)\cos x}\ dx$.
Evaluate $\displaystyle\int^{\dfrac{\pi}{4}}_0 \dfrac{x}{(\sin x+\cos x)\cos x}\ dx$.
Solving for this problem is a breeze if you're someone who is so sensitive about the possibility of the existence of property of symmetry for the integrand function involved.
Solving for this problem is a breeze if you're someone who is so sensitive about the possibility of the existence of property of symmetry for the integrand function involved.
Second Solution: IMO Solving Equation Problem: Solve the equation $x+a^3=\sqrt[3]{a-x}$ where a is real.
Solve the equation $x+a^3=\sqrt[3]{a-x}$ where a is real parameter.
My solution:
By observation, note that $x=a-a^3$ is a real solution for the equation $x+a^3=\sqrt[3]{a-x}$.
My solution:
By observation, note that $x=a-a^3$ is a real solution for the equation $x+a^3=\sqrt[3]{a-x}$.
IMO Solving Equation Problem: Solve the equation $x+a^3=\sqrt[3]{a-x}$ where a is real (First Solution)
Solve the equation $x+a^3=\sqrt[3]{a-x}$ where $a$ is real.
If one wants to do things in haste and quickly solve the above equation for $x$ without thinking much, one would definitely raise both sides of the equation to the third power to get rid of the cube root:
$x+a^3=\sqrt[3]{a-x}$
$(x+a^3)^3=(\sqrt[3]{a-x})^3$
If one wants to do things in haste and quickly solve the above equation for $x$ without thinking much, one would definitely raise both sides of the equation to the third power to get rid of the cube root:
$x+a^3=\sqrt[3]{a-x}$
$(x+a^3)^3=(\sqrt[3]{a-x})^3$
Optimization Contest Problem: Prove $x^4+x^3-x^2-x+1>0$ for all real $x$.
In one of my previous blog posts(optimization-contest-problem), we want to prove that [MATH]\color{yellow}\bbox[5px,blue]{x^4+x^3-x^2-x+1}[/MATH] is always greater than zero for all real $x$, or more specifically, for $x\gt 1$.
Classic Trigonometric Olympiad Problem: Evaluate $(1+\tan 1^{\circ})(1+\tan 2^{\circ})\cdots(1+\tan 43^{\circ})(1+\tan 44^{\circ})(1+\tan 45^{\circ})$
In this blog post, we will continue to manipulate the number one to looking for the most efficient and effective solution.
According to Wikipedia (Number One):
One, sometimes referred to as unity, is the integer before two and after zero. One is the first non-zero number in the natural numbers as well as the first odd number in the natural numbers.
According to Wikipedia (Number One):
One, sometimes referred to as unity, is the integer before two and after zero. One is the first non-zero number in the natural numbers as well as the first odd number in the natural numbers.
21th USA Mathematical Olympiad 1992 Problem
In the (previous blog post), we were asked to prove a 21th USA Mathematical Olympiad 1992 Problem:
Let $k=1^{\circ}$, show that [MATH]\sum_{n=0}^{88}\dfrac{1}{\cos (nk) \cos(n+1)k}=\dfrac{\cos k}{\sin^2 k}[/MATH]
But we have already worked out an trigonometric identity where:
$\dfrac{\sin 1^{\circ}}{\sin x^{\circ} \sin (x^{\circ}+1^{\circ})}=\cot x^{\circ}-\cot (x^{\circ}+1^{\circ})$
Let $k=1^{\circ}$, show that [MATH]\sum_{n=0}^{88}\dfrac{1}{\cos (nk) \cos(n+1)k}=\dfrac{\cos k}{\sin^2 k}[/MATH]
But we have already worked out an trigonometric identity where:
$\dfrac{\sin 1^{\circ}}{\sin x^{\circ} \sin (x^{\circ}+1^{\circ})}=\cot x^{\circ}-\cot (x^{\circ}+1^{\circ})$
Analysis for Quiz 12: Brain Power Enrichment Quiz (I)
Analysis for Quiz 12: Brain Power Enrichment Quiz (I)
Question 1: If $a\gt b$ and $c\gt d$ are true, then we can say $a+c\gt b+d$ is always true.
A. Correct.
B. Incorrect.
Answer:
Yes, that is always correct, regardless if $a,\,b,\,c,\,d$ are negative or positive real number.
Take for example, we have:
Question 1: If $a\gt b$ and $c\gt d$ are true, then we can say $a+c\gt b+d$ is always true.
A. Correct.
B. Incorrect.
Answer:
Yes, that is always correct, regardless if $a,\,b,\,c,\,d$ are negative or positive real number.
Take for example, we have:
How to make use of 1 in helping us to solve International Math Olympiad problem?
Here is another blog post that describes how we could use the figure $1$ in solving intriguing International Olympiad Mathematical Problems.
According to wikipedia (number one (1)):
According to wikipedia (number one (1)):
Algebraic Manipulation Skill II
Another algebraic manipulation skill that I want to share with students today:
Rewrite $a^2c^2+b^2c^2+a^2d^2+b^2d^2$ as the sum of two squares.
The vast majority students would say, hey! Isn't it obvious that we can factor out $a^2$ in $a^2c^2+a^2d^2$ and $b^2$ in $b^2c^2+b^2d^2$ such that we get:
Rewrite $a^2c^2+b^2c^2+a^2d^2+b^2d^2$ as the sum of two squares.
The vast majority students would say, hey! Isn't it obvious that we can factor out $a^2$ in $a^2c^2+a^2d^2$ and $b^2$ in $b^2c^2+b^2d^2$ such that we get:
Learning Algebraic Manipulation Skills
Some algebraic manipulation skills that you could learn by watching me doing it and it is going to be very rewarding if you know when to utilize these skills and use them to your advantage.
I'm sure you're pretty familiar with factoring sum and difference of squares or even cubes and recognizing perfect squares at first glance, take for example, when you see
I'm sure you're pretty familiar with factoring sum and difference of squares or even cubes and recognizing perfect squares at first glance, take for example, when you see
Analysis for Quiz 11: Creative Problem Solving
Analysis for Quiz 11: Creative Problem Solving
Question 1: Do you think we can factor part of the expression in the given equation $4x^2+5xy-6y^2-4x+3y-1=0$?
A. Yes.
B. No.
C. Perhaps.
Question 1: Do you think we can factor part of the expression in the given equation $4x^2+5xy-6y^2-4x+3y-1=0$?
A. Yes.
B. No.
C. Perhaps.
Solve in positive integers the equation $ab(a+b-10)+21a-3a^2+16b-2b^2=60$: First Solution (Continued)
I want to apology for posting the unfinished blog post on last Saturday (solve-in-positive-integers-equation.html), and I am truly sorry for that.
Here is the other part of the solution that I unwittingly left out.
Here is the other part of the solution that I unwittingly left out.
Potential Flaw in The Second Solution for the problem $ab(a+b-10)+21a-3a^2+16b-2b^2=60$.
Solve in positive integers the equation $ab(a+b-10)+21a-3a^2+16b-2b^2=60$.
In this blog post, I will discuss why the last step in my attempt to look for the positive integers $a$ and $b$ doesn't sound so right.
In this blog post, I will discuss why the last step in my attempt to look for the positive integers $a$ and $b$ doesn't sound so right.
Solve in positive integers the equation $ab(a+b-10)+21a-3a^2+16b-2b^2=60$ Second Solution
Solve in positive integers the equation $ab(a+b-10)+21a-3a^2+16b-2b^2=60$.
Second solution:
This second solution is much neater than the first, but in solving mathematical problems, solving it is what matters, isn't it? :D
Second solution:
This second solution is much neater than the first, but in solving mathematical problems, solving it is what matters, isn't it? :D
Solve in positive integers the equation $ab(a+b-10)+21a-3a^2+16b-2b^2=60$: First Solution
Determine if $n^2-21n+111$ is or is not a perfect square (Why the second solution fails?)
Determine if $n^2-21n+111$ is or is not a perfect square.
Answer:
Previously I wanted you to find the answer and explain back to me why the following solution cannot be deemed to be a sound solution.
Answer:
Previously I wanted you to find the answer and explain back to me why the following solution cannot be deemed to be a sound solution.
Determine if $n^2-21n+111$ is or is not a perfect square (Second Solution ?)
Determine if $n^2-21n+111$ is or is not a perfect square.
Answer:
I want you to consider the following method of attacking the problem, and digest it, then think about it long enough so you have found the answer and explain back to me why it cannot deem to be a solution.
I first treat $n^2-21n+111$ as a square, says $m^2$ and I then rewrite $n^2-21n+111$ in the following fashion:
Answer:
I want you to consider the following method of attacking the problem, and digest it, then think about it long enough so you have found the answer and explain back to me why it cannot deem to be a solution.
I first treat $n^2-21n+111$ as a square, says $m^2$ and I then rewrite $n^2-21n+111$ in the following fashion:
Making decision by weighing the data
Solve for all 6 complex roots of the equation $x^6+10x^5+70x^4+288x^3+880x^2+1600x+1792=0$.
Previously we talked about how to assign $2^8(7)$ to be the constants for the three factors such that we have
$\small x^6+10x^5+70x^4+288x^3+880x^2+1600x+2^8(7)=(x^2+ax+?)(x^2+bx+?)(x^2+cx+?)$
We realized that we would get to correctly assign the number as the constants for the three factors if we have got lucky, what if we don't have the luck and have to exhaust all possibility?
As the math educator, I would ask you to stop solving for this problem for a short while and turn your focus to asking students the number of cases that are possible to rewrite $2^8(7)$ as the product of three positive integers.
Let your students to shift their mind from algebra to probability, this often generates a good course for students as in real life, we have to deal with the situation where we have to consider many aspects so to suggest good solutions than coming up with approach that would waste our precious time and effort hugely.
We could, list out all the possible cases and do it like follows:
For [MATH]\color{yellow}\bbox[5px,purple]{2^8(7)=1(7)(2^8)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=(2^1)(7)(2^7)\\&=(2^2)(7)(2^6)\\ &=(2^3)(7)(2^5)\\ &=\cancel{(2^5)(7)(2^3)}\end{align*}\end{array}\right\}\text{3 cases}[/MATH]
For [MATH]\color{yellow}\bbox[5px,green]{2^8(7)=1(7\cdot 2)(2^7)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2)(2^7)\\&=(2^1)(7\cdot 2)(2^6)\\ &=(2^2)(7\cdot 2)(2^5)\\ &=(2^3)(7\cdot 2)(2^4)\\&=\cancel{(2^4)(7\cdot 2)(2^3)}\end{align*}\end{array}\right\}\text{4 cases}[/MATH]
For [MATH]\color{black}\bbox[5px,orange]{2^8(7)=1(7\cdot 2^2)(2^6)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^2)(2^6)\\&=(2^1)(7\cdot 2^2)(2^5)\\ &=(2^2)(7\cdot 2^2)(2^4)\\ &=(2^3)(7\cdot 2^2)(2^3)\\&=\cancel{(2^4)(7\cdot 2^2)(2^2)}\end{align*}\end{array}\right\}\text{4 cases}[/MATH]
For [MATH]\color{yellow}\bbox[5px,blue]{2^8(7)=1(7\cdot 2^3)(2^6)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^3)(2^5)\\&=(2^1)(7\cdot 2^3)(2^4)\\ &=(2^2)(7\cdot 2^3)(2^3)\\ &=(2^3)(7\cdot 2^3)(2^2)\\&=\cancel{(2^4)(7\cdot 2^3)(2^1)}\end{align*}\end{array}\right\}\text{4 cases}[/MATH]
For [MATH]\color{yellow}\bbox[5px,red]{2^8(7)=1(7\cdot 2^4)(2^4)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^4)(2^4)\\&=(2^1)(7\cdot 2^4)(2^3)\\ &=(2^2)(7\cdot 2^4)(2^2)\\ &=\cancel{(2^3)(7\cdot 2^4)(2^1)}\end{align*}\end{array}\right\}\text{3 cases}[/MATH]
For [MATH]\color{yellow}\bbox[5px,indigo]{2^8(7)=1(7\cdot 2^5)(2^3)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^5)(2^3)\\&=(2^1)(7\cdot 2^5)(2^2)\\ &=\cancel{(2^2)(7\cdot 2^5)(2^1)}\end{align*}\end{array}\right\}\text{2 cases}[/MATH]
For [MATH]\color{black}\bbox[5px,yellow]{2^8(7)=1(7\cdot 2^6)(2^2)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^6)(2^2)\\&=(2^1)(7\cdot 2^6)(2^1)\\ &=\cancel{(2^2)(7\cdot 2^5)(2^1)}\end{align*}\end{array}\right\}\text{2 cases}[/MATH]
For [MATH]\color{black}\bbox[5px,orange]{2^8(7)=1(7\cdot 2^7)(2)}[/MATH], we only have one case for that.
Similarly for [MATH]\color{white}\bbox[5px,purple]{2^8(7)=1(7\cdot 2^8)(1)}[/MATH], we only have one case for that.
So altogether, we would end up with a total of 26 possible cases to work.
Now, ask yourself by answer to yourself honestly, do you really want to work out all those 26 cases to look for the right answer to factor
$\small x^6+10x^5+70x^4+288x^3+880x^2+1600x+2^8(7)=(x^2+ax+?)(x^2+bx+?)(x^2+cx+?)$?
I'm fairly certain that you would beg for another alternative and put this one under the carpet by now. :D
Previously we talked about how to assign $2^8(7)$ to be the constants for the three factors such that we have
$\small x^6+10x^5+70x^4+288x^3+880x^2+1600x+2^8(7)=(x^2+ax+?)(x^2+bx+?)(x^2+cx+?)$
We realized that we would get to correctly assign the number as the constants for the three factors if we have got lucky, what if we don't have the luck and have to exhaust all possibility?
As the math educator, I would ask you to stop solving for this problem for a short while and turn your focus to asking students the number of cases that are possible to rewrite $2^8(7)$ as the product of three positive integers.
Let your students to shift their mind from algebra to probability, this often generates a good course for students as in real life, we have to deal with the situation where we have to consider many aspects so to suggest good solutions than coming up with approach that would waste our precious time and effort hugely.
We could, list out all the possible cases and do it like follows:
For [MATH]\color{yellow}\bbox[5px,purple]{2^8(7)=1(7)(2^8)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=(2^1)(7)(2^7)\\&=(2^2)(7)(2^6)\\ &=(2^3)(7)(2^5)\\ &=\cancel{(2^5)(7)(2^3)}\end{align*}\end{array}\right\}\text{3 cases}[/MATH]
For [MATH]\color{yellow}\bbox[5px,green]{2^8(7)=1(7\cdot 2)(2^7)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2)(2^7)\\&=(2^1)(7\cdot 2)(2^6)\\ &=(2^2)(7\cdot 2)(2^5)\\ &=(2^3)(7\cdot 2)(2^4)\\&=\cancel{(2^4)(7\cdot 2)(2^3)}\end{align*}\end{array}\right\}\text{4 cases}[/MATH]
For [MATH]\color{black}\bbox[5px,orange]{2^8(7)=1(7\cdot 2^2)(2^6)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^2)(2^6)\\&=(2^1)(7\cdot 2^2)(2^5)\\ &=(2^2)(7\cdot 2^2)(2^4)\\ &=(2^3)(7\cdot 2^2)(2^3)\\&=\cancel{(2^4)(7\cdot 2^2)(2^2)}\end{align*}\end{array}\right\}\text{4 cases}[/MATH]
For [MATH]\color{yellow}\bbox[5px,blue]{2^8(7)=1(7\cdot 2^3)(2^6)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^3)(2^5)\\&=(2^1)(7\cdot 2^3)(2^4)\\ &=(2^2)(7\cdot 2^3)(2^3)\\ &=(2^3)(7\cdot 2^3)(2^2)\\&=\cancel{(2^4)(7\cdot 2^3)(2^1)}\end{align*}\end{array}\right\}\text{4 cases}[/MATH]
For [MATH]\color{yellow}\bbox[5px,red]{2^8(7)=1(7\cdot 2^4)(2^4)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^4)(2^4)\\&=(2^1)(7\cdot 2^4)(2^3)\\ &=(2^2)(7\cdot 2^4)(2^2)\\ &=\cancel{(2^3)(7\cdot 2^4)(2^1)}\end{align*}\end{array}\right\}\text{3 cases}[/MATH]
For [MATH]\color{yellow}\bbox[5px,indigo]{2^8(7)=1(7\cdot 2^5)(2^3)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^5)(2^3)\\&=(2^1)(7\cdot 2^5)(2^2)\\ &=\cancel{(2^2)(7\cdot 2^5)(2^1)}\end{align*}\end{array}\right\}\text{2 cases}[/MATH]
For [MATH]\color{black}\bbox[5px,yellow]{2^8(7)=1(7\cdot 2^6)(2^2)}[/MATH], we could split it down to such cases:
[MATH]\left.\begin{array}{I}\begin{align*}2^8(7)&=1(7\cdot 2^6)(2^2)\\&=(2^1)(7\cdot 2^6)(2^1)\\ &=\cancel{(2^2)(7\cdot 2^5)(2^1)}\end{align*}\end{array}\right\}\text{2 cases}[/MATH]
For [MATH]\color{black}\bbox[5px,orange]{2^8(7)=1(7\cdot 2^7)(2)}[/MATH], we only have one case for that.
Similarly for [MATH]\color{white}\bbox[5px,purple]{2^8(7)=1(7\cdot 2^8)(1)}[/MATH], we only have one case for that.
So altogether, we would end up with a total of 26 possible cases to work.
Now, ask yourself by answer to yourself honestly, do you really want to work out all those 26 cases to look for the right answer to factor
$\small x^6+10x^5+70x^4+288x^3+880x^2+1600x+2^8(7)=(x^2+ax+?)(x^2+bx+?)(x^2+cx+?)$?
I'm fairly certain that you would beg for another alternative and put this one under the carpet by now. :D
Solve for all 6 complex roots of the equation $x^6+10x^5+70x^4+288x^3+880x^2+1600x+1792=0$ (Heuristic Solution)
Solve for all 6 complex roots of the equation $x^6+10x^5+70x^4+288x^3+880x^2+1600x+1792=0$.
My solution:
My solution:
Solve for all 6 complex roots of the equation $x^6+10x^5+70x^4+288x^3+880x^2+1600x+1792=0$ (First attempt at solution)
Solve for all 6 complex roots of the equation $x^6+10x^5+70x^4+288x^3+880x^2+1600x+1792=0$.
The most common method that students would think of how to tackle this problem is by setting up three factors, toying around the possible candidates for the constants for each factor as the prime factorization of $1792=2^8(7)$.
The most common method that students would think of how to tackle this problem is by setting up three factors, toying around the possible candidates for the constants for each factor as the prime factorization of $1792=2^8(7)$.
Prove that $ab\leq \dfrac {1}{8}$ (Third Solution)
Given $b^2-4ac$ is a real root of equation $ax^2+bx+c=0,\,\, (a\neq 0)$. Prove that $ab\leq \dfrac {1}{8}$.
Third solution:
Third solution:
Prove that $ab\leq \dfrac {1}{8}$ (Second Solution)
Second solution is my solution: (I want to mention it here that the first solution is provided by a Taiwan friend of mine)
Multiply the equation of $ax^2+bx+c=0$ by $4a$, we get:
Prove that $ab\leq \dfrac {1}{8}$ (First Solution)
Some students would find that this problem very confusing, as they have been told countless time that $b^2-4ac$ is actually a discriminant for the quadratic equation $ax^2+bx+c=0$.
In this instance, $b^2-4ac$ is both the discriminant and the root, they would think instantly something that looks like the following:
Fill up grids such that $\dfrac{\square}{\square \square}+\dfrac{\square}{\square \square} +\dfrac{\square}{\square\square}=1$
In the following grid, fill up the numbers from 1 to 9 (without repetition) such that their sum is $1$.
$\dfrac{\square}{\square \square}+\dfrac{\square}{\square \square} +\dfrac{\square}{\square\square}=1$
Solution provided by Mark, another contributor of this blog:
$\dfrac{\square}{\square \square}+\dfrac{\square}{\square \square} +\dfrac{\square}{\square\square}=1$
Solution provided by Mark, another contributor of this blog:
Analysis for Quiz 10: Training For Problem Solving Skills
The questions I want to give something to ponder, something that is not immediately straightforward, and some cool and rational thought will be required to answer the question.
Admittedly, I've touched a modicum bit in this regard at this slideshow (http://masteringolympiadmathematics.blogspot.com/2015/06/slideshow-9-creative-teaching.html), you could, if you want to refer it and answer the following quiz questions.
Question 1: What is the next square number after $(x-6)^4$?
$((x-6)^2)^2+1$
$((x-6+1)^2)^2$
$((x-6)^2+1)^2$
Answer:
Admittedly, I've touched a modicum bit in this regard at this slideshow (http://masteringolympiadmathematics.blogspot.com/2015/06/slideshow-9-creative-teaching.html), you could, if you want to refer it and answer the following quiz questions.
Question 1: What is the next square number after $(x-6)^4$?
$((x-6)^2)^2+1$
$((x-6+1)^2)^2$
$((x-6)^2+1)^2$
Answer:
Optimization Contest Problem: Find the maximum of f(x) (Heuristic Solution)
Find the maximum of $f(x) = \dfrac{x^4-x^2}{x^6+2x^3-1}$ where $x>1$.
If we want to maximize $f(x)=\dfrac{x^4-x^2}{x^6+2x^3-1}=\dfrac{1}{\left(\dfrac{x^6+2x^3-1}{x^4-x^2}\right)}$, this could be done if we are to find the minimum value for the expression $\dfrac{x^6+2x^3-1}{x^4-x^2}$.
Note that
Optimization Contest Problem: Find the maximum of f(x): Why The Second Solution Fails?
Find the maximum of $f(x) = \dfrac{x^4-x^2}{x^6+2x^3-1}$ where $x>1$.
Previously, we discussed how to avoid using the surest and safest way of approaching this particular problem with the calculus method and opted for the inequality method.
To recap, here is what we have gotten:
Previously, we discussed how to avoid using the surest and safest way of approaching this particular problem with the calculus method and opted for the inequality method.
To recap, here is what we have gotten:
Optimization Contest Problem: Find the maximum of f(x): Second Solution
Find the maximum of $f(x) = \dfrac{x^4-x^2}{x^6+2x^3-1}$ where $x>1$.
In my previous post(optimization-contest-problem), I showed you the way of approaching this particular problem with the most comfortable and familiar method (calculus method) that it would spring first to students' mind, a method that students' from all four corners of the world are inclined to use.
In my previous post(optimization-contest-problem), I showed you the way of approaching this particular problem with the most comfortable and familiar method (calculus method) that it would spring first to students' mind, a method that students' from all four corners of the world are inclined to use.
Optimization Contest Problem: Find the maximum of f(x): First Solution
Find the maximum of $f(x) = \dfrac{x^4-x^2}{x^6+2x^3-1}$ where $x>1$.
This is an excellent problem that could help in effective questioning so to get students fully understand some particular mathematics concepts and how to resolve optimization problem beautifully yet effectively.
But one may be tempted to solve it using the calculus method, as that is what teachers taught them what to do whenever we are to ask to find the maximum of a function, yes, calculus method works wonder and I will let you to decide, after showing you ways of approaching this problem so that you know how much this problem means as the best quality problem that enable us to activate and connect various areas in our brain and therefore think creatively.
This is an excellent problem that could help in effective questioning so to get students fully understand some particular mathematics concepts and how to resolve optimization problem beautifully yet effectively.
But one may be tempted to solve it using the calculus method, as that is what teachers taught them what to do whenever we are to ask to find the maximum of a function, yes, calculus method works wonder and I will let you to decide, after showing you ways of approaching this problem so that you know how much this problem means as the best quality problem that enable us to activate and connect various areas in our brain and therefore think creatively.
USA Mathematical Olympiad 1989 Problem (Third Method)
Which is larger, the real root of $x + x^2 + ... + x^8 = 8 - 10x^9$, or the real root of $x + x^2 + ... + x^{10} = 8 - 10x^{11}$?
My solution:
First, notice that
$1-x^9=(1-x)(x+x^2+\cdots+x^8)$
$1-x^9=(1-x)(8-10x^9)$
$1-x^9=8-10x^9-8x+10x^{10}$
$10x^{10}-9x^9-8x+7=0$
Whereas
$1-x^{11}=(1-x)(x+x^2+\cdots+x^{10})$
$1-x^{11}=(1-x)(8-10x^{11})$
$1-x^{11}=8-10x^{11}-8x+10x^{12}$
$10x^{12}-9x^{11}-8x+7=0$
So I let
$f(x)=10x^{10}-9x^9-8x+7$ and $g(x)=10x^{12}-9x^{11}-8x+7$.
Descartes's Rule says $f(x)$ has at most two positive real roots and obviously $x=1$ is one of the root of $f(x)$ and the Intermediate Value theorem tells us the other root lies between $(0, 0.95)$ since $f(0)\cdot f(0.95)=7(-0.28)\lt 0$.
Similarly, Descartes's Rule says $g(x)$ has two positive real roots and obviously $x=1$ is one of the root of $g(x)$ and the Intermediate Value theorem tells us the other root lies between $(0, 0.95)$ since $g(0)\cdot g(0.95)=7(-0.316)\lt 0$.
Observe also that
$\begin{align*}g(x)&=10x^{12}-9x^{11}-8x+7\\&=x^2(10x^{10}-9x^9-8x+7)-8x+7+8x^3-7x^2\\&=x^2f(x)+(8x-7)(x^2-1)\end{align*}$
If $a$ is a root of the function of $f$, that means $f(a)=0$, then we have:
$\begin{align*}g(a)&=a^2f(a)+(8a-7)(a^2-1)\\&=0+(8a-7)(a^2-1)\\&=(8a-7)(a^2-1)\end{align*}$
And here is a rough sketch of the graph $g(a)=(8a-7)(a^2-1)$
So, if $\dfrac{7}{8}\lt a\lt 1$, then $g(a)\lt 0$ and it follows that the real root of $x + x^2 + ... + x^8 = 8 - 10x^9$ is greater than the real root of $x + x^2 + ... + x^{10} = 8 - 10x^{11}$.
Whereas if $0\lt a\lt \dfrac{7}{8}$, then $g(a)\gt 0$, that will suggest the real root of $x + x^2 + ... + x^8 = 8 - 10x^9$ is less than the real root of $x + x^2 + ... + x^{10} = 8 - 10x^{11}$.
Now, our objective is to find out whether the root of the function of $f$ is greater than or less than $\dfrac{7}{8}$ so we can determine if the real root of $f(x)$ or $g(x)$ is greater.
$f(\dfrac{7}{8})=10(\dfrac{7}{8})^{10}-9(\dfrac{7}{8})^9-8(\dfrac{7}{8})+7=-0.075$
$f(\dfrac{6}{8})=10(\dfrac{6}{8})^{10}-9(\dfrac{6}{8})^9-8(\dfrac{6}{8})+7=0.8873$
Hence, we can say, based on the Intermediate Value theorem that the other positive real root of $f$, i.e. $a$, lies between $\dfrac{6}{8}$ and $\dfrac{7}{8}$, i.e. $a$ is less than $\dfrac{7}{8}$.
Therefore, we have proved that the real root of $x + x^2 + ... + x^8 = 8 - 10x^9$ is less than the real root of $x + x^2 + ... + x^{10} = 8 - 10x^{11}$.
USA Mathematical Olympiad 1989 Problem (Second Method)
USA Mathematical Olympiad 1989 Problem
Which is larger, the real root of $x + x^2 + ... + x^8 = 8 - 10x^9$, or the real root of $x + x^2 + ... + x^{10} = 8 - 10x^{11}$?
Previously we checked for the maximum and minimum points to ascertain if the first derivative of $f(x)=x+x^2+\cdots +x^8 +10x^9 - 8$ and $g(x)=x+x^2+\cdots +x^{10}+10x^{11}-8$ are always greater than or equal to zero.
Which is larger, the real root of $x + x^2 + ... + x^8 = 8 - 10x^9$, or the real root of $x + x^2 + ... + x^{10} = 8 - 10x^{11}$?
Previously we checked for the maximum and minimum points to ascertain if the first derivative of $f(x)=x+x^2+\cdots +x^8 +10x^9 - 8$ and $g(x)=x+x^2+\cdots +x^{10}+10x^{11}-8$ are always greater than or equal to zero.
USA Mathematical Olympiad 1989 Problem
USA Mathematical Olympiad 1989 Problem
Which is larger, the real root of $x + x^2 + ... + x^8 = 8 - 10x^9$, or the real root of $x + x^2 + ... + x^{10} = 8 - 10x^{11}$?
The upper part of the solution below is mine and the lower part belongs to the math professor from Arizona, USA.
Which is larger, the real root of $x + x^2 + ... + x^8 = 8 - 10x^9$, or the real root of $x + x^2 + ... + x^{10} = 8 - 10x^{11}$?
The upper part of the solution below is mine and the lower part belongs to the math professor from Arizona, USA.
IMO contest problem (Second solution) Prove that $a^2+b^4=1994$
Let $a,\,b$ be positive integers with $b\gt3$ and $a^2+b^4=2((a-6)^2+(b+1)^2)$.
Prove that $a^2+b^4=1994$.
The solution below is provided by the retired math professor from the U.K. In my opinion, this solution is more easy to follow than the previously discussed, but credit must be given to both as they are equally insightful and neat solutions.
Prove that $a^2+b^4=1994$.
The solution below is provided by the retired math professor from the U.K. In my opinion, this solution is more easy to follow than the previously discussed, but credit must be given to both as they are equally insightful and neat solutions.
Let $a,\,b$ be positive integers with $b>3$ and $a^2+b^4=2((a-6)^2+(b+1)^2)$. Prove that $a^2+b^4=1994$.
Let $a,\,b$ be positive integers with $b>3$ and $a^2+b^4=2((a-6)^2+(b+1)^2)$.
Prove that $a^2+b^4=1994$.
This is a genuinely hard problem. If you are smart, you will wonder and ask your teacher if this question is saying there is only one solution for $(a,\,b)$ such that there is only a value for $a^2+b^4$, and that must be $1994$.
Yes, your intuition is right, the question is, how to find that only solution for both $a$ and $b$ from the only given single equation?
Prove that $a^2+b^4=1994$.
This is a genuinely hard problem. If you are smart, you will wonder and ask your teacher if this question is saying there is only one solution for $(a,\,b)$ such that there is only a value for $a^2+b^4$, and that must be $1994$.
Yes, your intuition is right, the question is, how to find that only solution for both $a$ and $b$ from the only given single equation?
Food for thought for both teachers and students
Food for thought:
It's rare that teachers will give something that are truly questioning and cultivating students' interest in math and science subjects. If math educators shift their teaching methodology towards more inquiry based teaching, and let students to take part by start thinking, improve their ability to think abstractly and multi-dimensionally, this will build strong foundation of math for students. This strong foundation will enable students to acquire higher-order skills needed for the 21st century and to becoming highly competent and extraordinary intelligent students that could always plan ahead, see the future consequences of an action, provide alternative explanation of events and reason more effectively.
It's rare that teachers will give something that are truly questioning and cultivating students' interest in math and science subjects. If math educators shift their teaching methodology towards more inquiry based teaching, and let students to take part by start thinking, improve their ability to think abstractly and multi-dimensionally, this will build strong foundation of math for students. This strong foundation will enable students to acquire higher-order skills needed for the 21st century and to becoming highly competent and extraordinary intelligent students that could always plan ahead, see the future consequences of an action, provide alternative explanation of events and reason more effectively.
Smartest Way of Solving Hardest Trigonometric Equation
$\sqrt{2} \cos \left(\dfrac{x}{5}-\dfrac{\pi }{12}\right)-\sqrt{6}\sin \left(\dfrac{x}{5}-\dfrac{\pi}{12}\right)=2\left(\sin \left((\dfrac{x}{5}-\dfrac{2\pi}{3}\right)-\sin \left((\dfrac{3x}{5}+\dfrac{\pi}{6}\right)\right)$
An excellent observation and hence sublimely insightful solution provided by one mathematicans from the England:
Hardest Trigonometric Equation (First Solution)
Solve the trigonometric equation.
$\small \sqrt{2} \cos \left(\dfrac{x}{5}-\dfrac{\pi }{12}\right)-\sqrt{6}\sin \left(\dfrac{x}{5}-\dfrac{\pi}{12}\right)=2\left(\sin \left(\dfrac{x}{5}-\dfrac{2\pi}{3}\right)-\sin \left(\dfrac{3x}{5}+\dfrac{\pi}{6}\right)\right)$
My solution:
By letting [MATH]A=\frac{x}{5}-\frac{\pi}{12}[/MATH] use the sum-to-product formula to simplify the LHS of the equation, I get:
$\small \sqrt{2} \cos \left(\dfrac{x}{5}-\dfrac{\pi }{12}\right)-\sqrt{6}\sin \left(\dfrac{x}{5}-\dfrac{\pi}{12}\right)=2\left(\sin \left(\dfrac{x}{5}-\dfrac{2\pi}{3}\right)-\sin \left(\dfrac{3x}{5}+\dfrac{\pi}{6}\right)\right)$
My solution:
By letting [MATH]A=\frac{x}{5}-\frac{\pi}{12}[/MATH] use the sum-to-product formula to simplify the LHS of the equation, I get:
Hardest Trigonometric Equation (2)
In today post, I will take up where we left off (effective-teaching-of-math), to continue solving the trigonometric equation
$\sqrt{2} \cos \left(\dfrac{x}{5}-\dfrac{\pi }{12}\right)-\sqrt{6}\sin \left(\dfrac{x}{5}-\dfrac{\pi}{12}\right)=2\left(\sin \left((\dfrac{x}{5}-\dfrac{2\pi}{3}\right)-\sin \left(\dfrac{3x}{5}+\dfrac{\pi}{6}\right)\right)$
The LHS of the equation has been simplified down to
$\sqrt{2} \cos \left(\dfrac{x}{5}-\dfrac{\pi }{12}\right)-\sqrt{6}\sin \left(\dfrac{x}{5}-\dfrac{\pi}{12}\right)=2\left(\sin \left((\dfrac{x}{5}-\dfrac{2\pi}{3}\right)-\sin \left(\dfrac{3x}{5}+\dfrac{\pi}{6}\right)\right)$
The LHS of the equation has been simplified down to
Effective Teaching of Math Using Hard Trigonometry Contest Problem
Many of the so-called practices/drills that are designed to achieve the learning for mastery are just near aimless activities, and genuine illumination of important mathematical ideas is rare, not to mention providing the opportunities of making students to think deeply, creatively and critically in generating solutions. There is a near obsession with calculators/ICT which preventing students from gaining a true mastery of basic skills. Overall, these practice problems are watered-down and less interesting math activities.
Given $x,\,y,\,z$ are real such that $2x+y+z+14=2\sqrt{2x}+4\sqrt{y+1}+6\sqrt{z-1}$. Evaluate $\dfrac{x-y}{z}$.
Given $x,\,y,\,z$ are real such that $2x+y+z+14=2\sqrt{2x}+4\sqrt{y+1}+6\sqrt{z-1}$.
Evaluate $\dfrac{x-y}{z}$.
My solution:
This IMO Problem should look easy to you if you're being careful and look at the problem with your heart and mind, not merely with the eyes.
For me, I will try to group
Evaluate $\dfrac{x-y}{z}$.
My solution:
This IMO Problem should look easy to you if you're being careful and look at the problem with your heart and mind, not merely with the eyes.
For me, I will try to group
Work backwards Putnam IMO Contest Problem
Putnam Contest Problem:
Evaluate [MATH]\int_{0}^{\dfrac{\pi}{2}} \dfrac{\cos^4 x+\sin x\cos^3x+\sin^2 x\cos^2 x+\sin^3x\cos x}{\sin^4 x+\cos^4 x+2\sin x\cos^3 x+2\sin^2 x\cos^2 x+2\sin^3 x\cos x}\,dx[/MATH].
Solution of mine, which is different from the previously posted method provided by Mark(putnam-contest-problem):
Evaluate [MATH]\int_{0}^{\dfrac{\pi}{2}} \dfrac{\cos^4 x+\sin x\cos^3x+\sin^2 x\cos^2 x+\sin^3x\cos x}{\sin^4 x+\cos^4 x+2\sin x\cos^3 x+2\sin^2 x\cos^2 x+2\sin^3 x\cos x}\,dx[/MATH].
Solution of mine, which is different from the previously posted method provided by Mark(putnam-contest-problem):
Creative Solution for IMO Trigonometry Problem
Let $A,\,B$ be acute angles such that $\tan B=2015\sin A \cos A-2015\sin^2 A \tan B$.
Find the greatest possible value of $\tan B$.
This blog post is to highlight the fact that if we're creative enough, we can avoid the tedious calculus method to look for the maximal of $\tan B$.
You have to be aware of a few things as well:
1.
When $B$ is an acute angle and if $\sin B\le \dfrac{m}{n}$, then $\tan B\le \dfrac{m}{\sqrt{n^2-m^2}}$ must be true.
In other words, we obtain the maximal of $\tan B$ if we have obtained the maximal of $\sin B$.
Find the greatest possible value of $\tan B$.
This blog post is to highlight the fact that if we're creative enough, we can avoid the tedious calculus method to look for the maximal of $\tan B$.
You have to be aware of a few things as well:
1.
When $B$ is an acute angle and if $\sin B\le \dfrac{m}{n}$, then $\tan B\le \dfrac{m}{\sqrt{n^2-m^2}}$ must be true.
In other words, we obtain the maximal of $\tan B$ if we have obtained the maximal of $\sin B$.
IMO (Hong Kong) Trigonometric Problem (Modified)
Let $A,\,B$ be acute angles such that $\tan B=2015\sin A \cos A-2015\sin^2 A \tan B$.
Find the greatest possible value of $\tan B$.
This is a fun IMO problem, since it has many ways (all are nothing less than remarkable) to approach it and without any further ado, I will post with the first approach here:
$\tan B=2015\sin A \cos A-2015\sin^2 A \tan B$
$\tan B(1+2015\sin^2 A )=2015\sin A \cos A$
Find the greatest possible value of $\tan B$.
This is a fun IMO problem, since it has many ways (all are nothing less than remarkable) to approach it and without any further ado, I will post with the first approach here:
$\tan B=2015\sin A \cos A-2015\sin^2 A \tan B$
$\tan B(1+2015\sin^2 A )=2015\sin A \cos A$
Another method to solve the summation series from Quiz 9
a
The summation of series from quiz 9 (quiz-9-mock-imo-algebra-contest) can be tackled using another method.
First, note that $n^2-2n+1,\,n^2-1,\,n^2+2n+1$ all can be factored as:
$n^2-2n+1=(n-1)^2$
$n^2-1=(n-1)(n+1)$
$n^2+2n+1=(n+1)^2$
First, note that $n^2-2n+1,\,n^2-1,\,n^2+2n+1$ all can be factored as:
$n^2-2n+1=(n-1)^2$
$n^2-1=(n-1)(n+1)$
$n^2+2n+1=(n+1)^2$
4th June 2015's Edexcel exam paper: The Probability of Hannah eating two orange sweets
This is the problem in full:
There are $n$ sweets in a bag. $6$ of the sweets are orange. The rest of the sweets are yellow. Hannah takes at random a sweet from the bag. She eats the sweet. Hannah then takes at random another sweet from the bag. She eats the sweet. The probability that Hannah eats two orange sweets is $\dfrac{1}{3}$.
a. Show that $n^2-n-90=0$.
b. Solve $n^2-n-90=0$ to find the value of $n$.
Here is how to tackle the problem using the tree diagram.
Analysis: Quiz 9 Mock IMO Algebra Contest
Sum the series below:
[MATH]\sum_{n=4}^{999}\dfrac{1}{\sqrt[3]{n^2-2n+1}+\sqrt[3]{n^2+2n+1}+\sqrt[3]{n^2-1}}.[/MATH]
Question 1: Do you think the expression on the denominator can be factored?
Yes.
No.
This is a really rich way to asking problem so we make the students to think deep before simply giving out the answer yes or no so easily.
[MATH]\sum_{n=4}^{999}\dfrac{1}{\sqrt[3]{n^2-2n+1}+\sqrt[3]{n^2+2n+1}+\sqrt[3]{n^2-1}}.[/MATH]
Question 1: Do you think the expression on the denominator can be factored?
Yes.
No.
This is a really rich way to asking problem so we make the students to think deep before simply giving out the answer yes or no so easily.
Labels:
common factor,
common ratio,
common term,
denominator,
factored,
first term,
geometric series,
IMO,
partial fraction,
rationalizing denominator,
rewrite,
series telescopes,
substitute,
sum the series
Third Method of Solving IMO Optimization Contest Problem: Find the minimum value of $xy$,
Third Method of Solving IMO Optimization Contest Problem:
Find the minimum value of $xy$, given that $x^2+y^2+z^2=7$, $xy+xz+yz=4$, and $x, y$ and $z$ are real numbers.
This third method is provided by Mark, another blog contributor and he approached the problem using the well-known Lagrange multipliers method:
Find the minimum value of $xy$, given that $x^2+y^2+z^2=7$, $xy+xz+yz=4$, and $x, y$ and $z$ are real numbers.
This third method is provided by Mark, another blog contributor and he approached the problem using the well-known Lagrange multipliers method:
Second Method of Solving IMO Optimization Contest Problem: Find minimum $xy$
Second Method of Solving IMO Optimization Contest Problem:
Find the minimum value of $xy$, given that $x^2+y^2+z^2=7$, $xy+xz+yz=4$, and $x, y$ and $z$ are real numbers.
The second method is the solution provided by a well-known mathematics retired professor from the University in the U.K.
Find the minimum value of $xy$, given that $x^2+y^2+z^2=7$, $xy+xz+yz=4$, and $x, y$ and $z$ are real numbers.
The second method is the solution provided by a well-known mathematics retired professor from the University in the U.K.
IMO Optimization Contest Problem: Find the minimum value of $xy$, given that $x^2+y^2+z^2=7$, $xy+xz+yz=4$, and $x, y$ and $z$ are real numbers.
IMO Optimization Contest Problem:
Find the minimum value of $xy$, given that $x^2+y^2+z^2=7$, $xy+xz+yz=4$, and $x, y$ and $z$ are real numbers.
My solution:
From the well-known identity
$(x+y+z)^2=x^2+y^2+z^2+2(xy+xz+yz)$
and the given values for $x^2+y^2+z^2=7$ and $xy+xz+yz=4$, we get:
$(x+y+z)^2=7+2(4)$
Find the minimum value of $xy$, given that $x^2+y^2+z^2=7$, $xy+xz+yz=4$, and $x, y$ and $z$ are real numbers.
My solution:
From the well-known identity
$(x+y+z)^2=x^2+y^2+z^2+2(xy+xz+yz)$
and the given values for $x^2+y^2+z^2=7$ and $xy+xz+yz=4$, we get:
$(x+y+z)^2=7+2(4)$
Putnam Contest Problem: Evaluate [MATH]\tiny \int_{0}^{\dfrac{\pi}{2}} \dfrac{\cos^4 x+\sin x\cos^3x+\sin^2 x\cos^2 x+\sin^3x\cos x}{\sin^4 x+\cos^4 x+2\sin x\cos^3 x+2\sin^2 x\cos^2 x+2\sin^3 x\cos x}\,dx[/MATH].
Putnam Contest Problem:
Evaluate [MATH] \int_{0}^{\dfrac{\pi}{2}} \dfrac{\cos^4 x+\sin x\cos^3x+\sin^2 x\cos^2 x+\sin^3x\cos x}{\sin^4 x+\cos^4 x+2\sin x\cos^3 x+2\sin^2 x\cos^2 x+2\sin^3 x\cos x}\,dx[/MATH].
Solution provided by Mark, another contributor of this blog.
Let:
[MATH]\small I= \int_{0}^{\frac{\pi}{2}} \frac{\cos^4(x)+\sin(x)\cos^3(x)+\sin^2(x)\cos^2(x)+\sin^3(x)\cos(x)}{\sin^4(x)+\cos^4(x)+2\sin(x)\cos^3 (x)+2\sin^2(x)\cos^2(x)+2\sin^3(x)\cos(x)}\,dx-(1)[/MATH]
Using the identity:
Evaluate [MATH] \int_{0}^{\dfrac{\pi}{2}} \dfrac{\cos^4 x+\sin x\cos^3x+\sin^2 x\cos^2 x+\sin^3x\cos x}{\sin^4 x+\cos^4 x+2\sin x\cos^3 x+2\sin^2 x\cos^2 x+2\sin^3 x\cos x}\,dx[/MATH].
Solution provided by Mark, another contributor of this blog.
Let:
[MATH]\small I= \int_{0}^{\frac{\pi}{2}} \frac{\cos^4(x)+\sin(x)\cos^3(x)+\sin^2(x)\cos^2(x)+\sin^3(x)\cos(x)}{\sin^4(x)+\cos^4(x)+2\sin(x)\cos^3 (x)+2\sin^2(x)\cos^2(x)+2\sin^3(x)\cos(x)}\,dx-(1)[/MATH]
Using the identity:
China IMO problem: Simplify $(ay+bx)^3-(ax+by)^3+(a^3-b^3)(x^3-y^3)$
Simplify $(ay+bx)^3-(ax+by)^3+(a^3-b^3)(x^3-y^3)$.
We know this is a trick problem because it couldn't be required us to expand all the three terms and then collect like terms to simplify it.
So, if we don't expand the expression, how are we going to simplify it?
We know this is a trick problem because it couldn't be required us to expand all the three terms and then collect like terms to simplify it.
So, if we don't expand the expression, how are we going to simplify it?
Mock IMO contest problem: Solve $8 x^4-3 x^3-464 x^2-850 x+384=0$.
Mock IMO contest problem:
Solve $8 x^4-3 x^3-464 x^2-850 x+384=0$.
Observe! The best problem solver is also the best observer, train your eyes to see things others won't necessarily see or on first glance. The eyes are the windows to everything.
We need to exercise our mind by solving intriguing challenges as they can certainly keep our brain sharp. Sharp mindedness means the quickness of a person to interpret, understand, analyze, or pick up an idea adequately. It is a quality that enables you to find a solution to a problem very quickly or answer a question very quickly or learn very quickly. A person with sharp brain is a keen and quick observer.
Solve $8 x^4-3 x^3-464 x^2-850 x+384=0$.
Observe! The best problem solver is also the best observer, train your eyes to see things others won't necessarily see or on first glance. The eyes are the windows to everything.
We need to exercise our mind by solving intriguing challenges as they can certainly keep our brain sharp. Sharp mindedness means the quickness of a person to interpret, understand, analyze, or pick up an idea adequately. It is a quality that enables you to find a solution to a problem very quickly or answer a question very quickly or learn very quickly. A person with sharp brain is a keen and quick observer.
China IMO Mock Problem: Given $xy$ is rational number, and $x$ and $y$ are the roots of the equations $6x^2+2015x+8=0$ and $6x^2+2015x+8=0$ respectively. Evaluate $\dfrac{x}{y}$.
Given $xy\ne 1$, and $x$ and $y$ are the roots of the equations $6x^2+2015x+8=0$ and $6x^2+2015x+8=0$ respectively. Evaluate $\dfrac{x}{y}$.
Solution:
Since the coefficients of $6x^2+2015x+8=0$ are the same as the coefficients of $8y^2+2015y+6$ in reversed order, and we're told that $x$ is the root of the equation $6x^2+2015x+8=0$ while $y$ is the root of the equation $8y^2+2015y+6$.
Edward Witten, the World's Greatest Living Theoretical Physicist
Source from Wikipedia (Edward_Witten):
Witten has been honored with numerous awards including a MacArthur Grant (1982), the Fields Medal (1990), the Nemmers Prize in Mathematics (2000), the National Medal of Science[18] (2002), Pythagoras Award[19] (2005), the Henri Poincaré Prize (2006), the Crafoord Prize (2008), the Lorentz Medal (2010) the Isaac Newton Medal (2010) and the Fundamental Physics Prize (2012). Since 1999, he has been a Foreign Member of the Royal Society (London).[20] Pope Benedict XVI appointed Witten as a member of the Pontifical Academy of Sciences (2006). He also appeared in the list of TIME magazine's 100 most influential people of 2004. In 2012 he became a fellow of the American Mathematical Society.
November 13, 2008 From Discover Magazine
Witten has been honored with numerous awards including a MacArthur Grant (1982), the Fields Medal (1990), the Nemmers Prize in Mathematics (2000), the National Medal of Science[18] (2002), Pythagoras Award[19] (2005), the Henri Poincaré Prize (2006), the Crafoord Prize (2008), the Lorentz Medal (2010) the Isaac Newton Medal (2010) and the Fundamental Physics Prize (2012). Since 1999, he has been a Foreign Member of the Royal Society (London).[20] Pope Benedict XVI appointed Witten as a member of the Pontifical Academy of Sciences (2006). He also appeared in the list of TIME magazine's 100 most influential people of 2004. In 2012 he became a fellow of the American Mathematical Society.
November 13, 2008 From Discover Magazine
Quiz 8: Edward Witten, the World's Greatest Living Theoretical Physicist
Solve $\sqrt{x+16}+\sqrt[4]{x+16}=12$.
Solve $\sqrt{x+16}+\sqrt[4]{x+16}=12$.
For some students, they would think to square the given equation three times to get rid of the fourth root and square root terms:
$\sqrt{x+16}+\sqrt[4]{x+16}=12$
$(\sqrt[4]{x+16})^2=(12-\sqrt{x+16})^2$
$\sqrt{x+16}=144-24\sqrt{x+16}+x+16$
For some students, they would think to square the given equation three times to get rid of the fourth root and square root terms:
$\sqrt{x+16}+\sqrt[4]{x+16}=12$
$(\sqrt[4]{x+16})^2=(12-\sqrt{x+16})^2$
$\sqrt{x+16}=144-24\sqrt{x+16}+x+16$
Other Heuristic Method to Prove the Given Expression Greater Than Zero
Given that $x\ne 0$ and $x$ is real that satisfies $\large \sqrt[3]{x^5-20x}=\sqrt[5]{x^3+20x}$. Find the product of all possible values of $x$.
Regarding to the previous blog post(china-imo-contest-problem) that I mentioned how to prove
$a^4+a^3 x+a^2 (x^2+1)+a x^3+x^4+x^2+a x> 0$ in
Regarding to the previous blog post(china-imo-contest-problem) that I mentioned how to prove
$a^4+a^3 x+a^2 (x^2+1)+a x^3+x^4+x^2+a x> 0$ in
China IMO Contest Problem: Given $\sqrt[3]{x^5-20x}=\sqrt[5]{x^3+20x}$. Find the product of all possible values of $x$.
Given that $x\ne 0$ and $x$ is real that satisfies $\large \sqrt[3]{x^5-20x}=\sqrt[5]{x^3+20x}$. Find the product of all possible values of $x$.
Answer:
Let $\large a=\sqrt[3]{x^5-20x}=\sqrt[5]{x^3+20x}$.
Consider $\large a=\sqrt[3]{x^5-20x}$, we have:
$\large a^3=x^5-20x---(1)$
Consider $\large a=\sqrt[5]{x^3+20x}$, we have:
Answer:
Let $\large a=\sqrt[3]{x^5-20x}=\sqrt[5]{x^3+20x}$.
Consider $\large a=\sqrt[3]{x^5-20x}$, we have:
$\large a^3=x^5-20x---(1)$
Consider $\large a=\sqrt[5]{x^3+20x}$, we have:
IMO Problem: If $\dfrac{(x-y)(y-z)(z-x)}{(x+y)(y+z)(z+x)}=\dfrac{2014}{2015}$, evaluate $\dfrac{x}{x+y}+\dfrac{y}{y+z}+\dfrac{z}{z+x}$.
We all know in solving this problem correctly, our method should focus on turning the given equation so that the LHS of the equation could be represented by the wanted expression. That is, we hope to turn $\dfrac{(x-y)(y-z)(z-x)}{(x+y)(y+z)(z+x)}=\dfrac{2014}{2015}$ so the LHS can take the form $\dfrac{x}{x+y}+\dfrac{y}{y+z}+\dfrac{z}{z+x}$.
2015 IMO contest problem: If$x,\,y,\,z$ are real numbers such that $x+2y+3z=6$ and $x^2+4y^2+9z^2=12$, evaluate $xyz$.
If$x,\,y,\,z$ are real numbers such that $x+2y+3z=6$ and $x^2+4y^2+9z^2=12$, evaluate $xyz$.
There is something that this Olympiad problem might trick us because it's obvious that $x^2,\,4y^2,\,9z^2$ are squares of $x,\,2y,\,3z$ and hence, one has reason to believe that the proper first step in solving this problem is to square the first given equation:
$x+2y+3z=6$
There is something that this Olympiad problem might trick us because it's obvious that $x^2,\,4y^2,\,9z^2$ are squares of $x,\,2y,\,3z$ and hence, one has reason to believe that the proper first step in solving this problem is to square the first given equation:
$x+2y+3z=6$
Putnam Math Exam Problem: Evaluate [MATH]\prod_{n=2}^{\infty}\frac{n^3-1}{n^3+1}[/MATH]
Putnam Math Exam Problem:
Evaluate [MATH]\prod_{n=2}^{\infty}\frac{n^3-1}{n^3+1}[/MATH].
I admit it, the first (or should I say, the only) thing that we could do about the given fraction's expression, is to factor it:
Evaluate [MATH]\prod_{n=2}^{\infty}\frac{n^3-1}{n^3+1}[/MATH].
I admit it, the first (or should I say, the only) thing that we could do about the given fraction's expression, is to factor it:
Second Solution to evaluate $\dfrac{\cos 1^{\circ}+\cos 2^{\circ}+\cdots+\cos 44^{\circ}}{\sin 1^{\circ}+\sin 2^{\circ}+\cdots+\sin 44^{\circ}}$
Express $\dfrac{\cos 1^{\circ}+\cos 2^{\circ}+\cdots+\cos 44^{\circ}}{\sin 1^{\circ}+\sin 2^{\circ}+\cdots+\sin 44^{\circ}}$ in the form $a+b\sqrt{c}$, where $a,\,b,\,c$ are positive integers.
Answer:
Other solution:
It's always better to rewrite the given expression so both numerator and denominator carry more terms for better visualization effect:
Answer:
Other solution:
It's always better to rewrite the given expression so both numerator and denominator carry more terms for better visualization effect:
Simplify $\dfrac{\cos 1^{\circ}+\cos 2^{\circ}+\cdots+\cos 44^{\circ}}{\sin 1^{\circ}+\sin 2^{\circ}+\cdots+\sin 44^{\circ}}$
Express $\dfrac{\cos 1^{\circ}+\cos 2^{\circ}+\cdots+\cos 44^{\circ}}{\sin 1^{\circ}+\sin 2^{\circ}+\cdots+\sin 44^{\circ}}$ in the form $a+b\sqrt{c}$, where $a,\,b,\,c$ are positive integers.
(This question showed up here(math-teacher-guide) but I did not include its solution in that slide show).
My solution:
Normally for simplifying trigonometric question such as this one, there is one thing that's so worth noticing:
(This question showed up here(math-teacher-guide) but I did not include its solution in that slide show).
My solution:
Normally for simplifying trigonometric question such as this one, there is one thing that's so worth noticing:
Slideshow 7: One Criterion of Mathematically Proficient Students
Method 2: Find x and y if $\dfrac{1}{1!21!}+\dfrac{1}{3!19!}+\dfrac{1}{5!17!}+\cdots+\dfrac{1}{21!1!}=\dfrac{2^x}{y!}$
Method 2:
Find x and y if $\dfrac{1}{1!21!}+\dfrac{1}{3!19!}+\dfrac{1}{5!17!}+\cdots+\dfrac{1}{21!1!}=\dfrac{2^x}{y!}$
If $x,\,y$ are positive integers such that $\dfrac{1}{1!21!}+\dfrac{1}{3!19!}+\dfrac{1}{5!17!}+\dfrac{1}{7!15!}+\dfrac{1}{9!13!}+\dfrac{1}{11!11!}+\dfrac{1}{13!9!}+\dfrac{1}{15!7!}+\dfrac{1}{17!5!}+\dfrac{1}{19!3!}+\dfrac{1}{21!1!}=\dfrac{2^x}{y!}$.
Find $x,\,y$.
Find $x,\,y$.
IMO Practice Problem: Find the exact real root for the equation $10x^3-12x^2-6x-1=0$
Find the exact real root for the equation $10x^3-12x^2-6x-1=0$.
The given cubic cannot be factored easily and beautifully, so the method of factoring the given polynomial is out of the question.
I hear you, the next best approach might be to try out the substitution method, with the hope that after the substitution, we have less variable terms in our newly set equation. But there seems no suitable substitution is available so to make simpler the given equation.
The given cubic cannot be factored easily and beautifully, so the method of factoring the given polynomial is out of the question.
I hear you, the next best approach might be to try out the substitution method, with the hope that after the substitution, we have less variable terms in our newly set equation. But there seems no suitable substitution is available so to make simpler the given equation.
Slideshow 6: Real World Application of Mathematics
Third Heuristic Method In Solving Problem: Compare $M$ and $N$.
The third inspiring methods of solving the above question will be discussed in this post.
It's solved by one Indian genius, a math friend of mine who compared the quantities between $M^4$ and $N^4$:
He first noticed
Second Heuristic Method In Solving Problem: Compare $M$ and $N$.
One of the other two inspiring methods of solving the above question will be discussed in this post.
When we're asked to compare two quantities, like in this instance, we have $M$ and $N$. But that doesn't restrict us in working and considering only with the linear power of $M$ and $N$.
Compare M and N
Given that $p,\,q,\,r,\,s,\,a,\,b$ are positive real numbers with $M=\sqrt{ap+br}\cdot \sqrt{\dfrac{q}{a}+\dfrac{s}{b}}$ and $N=\sqrt{pq}+\sqrt{rs}$. Compare $M$ and $N$.
This question has the best form of quality because it allows us to approach it in at least 3 different ways, 3 of which that are enlighting and inspiring.
This question has the best form of quality because it allows us to approach it in at least 3 different ways, 3 of which that are enlighting and inspiring.
Mock Olympiad Math Problem: Solve $\large 3^{\sin^4 x-\cos^2 x}-3^{\cos^4 x-\sin^2 x}=\cos 2x$.
Solve $\large 3^{\sin^4 x-\cos^2 x}-3^{\cos^4 x-\sin^2 x}=\cos 2x$.
$\large 3^{\sin^4 x-\cos^2 x}-3^{\cos^4 x-\sin^2 x}=\cos 2x$
$\large 3^{\sin^4 x-\cos^2 x}\left(1-\dfrac{3^{\cos^4 x-\sin^2 x}}{3^{\sin^4 x-\cos^2 x}}\right)=\cos 2x$
$\large 3^{\sin^4 x-\cos^2 x}-3^{\cos^4 x-\sin^2 x}=\cos 2x$
$\large 3^{\sin^4 x-\cos^2 x}\left(1-\dfrac{3^{\cos^4 x-\sin^2 x}}{3^{\sin^4 x-\cos^2 x}}\right)=\cos 2x$
Another method to prove $7 ≥ \sqrt 2+\sqrt 5 + \sqrt {11}$
Show with proof which of these two values is smaller:
$7$, or $\sqrt 2+\sqrt 5 + \sqrt {11}$
In my (few) previous blog post (Which is greater), I mentioned of how I proved for $\sqrt 2+\sqrt 5 + \sqrt {11}$ is smaller than $7$.
But that doesn't mean that solution is the only way out to prove for that kind of problem.
$7$, or $\sqrt 2+\sqrt 5 + \sqrt {11}$
In my (few) previous blog post (Which is greater), I mentioned of how I proved for $\sqrt 2+\sqrt 5 + \sqrt {11}$ is smaller than $7$.
But that doesn't mean that solution is the only way out to prove for that kind of problem.
Analysis Quiz 7: IMO Mock Trigonometric Math Quiz
Analysis Quiz 6:
IMO Mock Trigonometric Math Quiz
Please answer the following questions based on the trigonometric equation below:
$\sin 9x-\csc^2 x=5\sin 3x+9\tan^2 x-1$
Question 1.
Would you convert the cosecant function to the sine function to solve the trigonometric equation above?
Yes.
No.
Perhaps.
Answer:
For an old hand like me (I'm not old at all, hehehe...), I could say right up front, loudly that I would not convert the cosecant function to the sine function in this case! But, if you are new and eager to learn, I will lead you to the answer, just that you have to be patient.
IMO Mock Trigonometric Math Quiz
Please answer the following questions based on the trigonometric equation below:
$\sin 9x-\csc^2 x=5\sin 3x+9\tan^2 x-1$
Question 1.
Would you convert the cosecant function to the sine function to solve the trigonometric equation above?
Yes.
No.
Perhaps.
Answer:
For an old hand like me (I'm not old at all, hehehe...), I could say right up front, loudly that I would not convert the cosecant function to the sine function in this case! But, if you are new and eager to learn, I will lead you to the answer, just that you have to be patient.
Show with proof which of these two values is smaller: $7$, or $\sqrt 2+\sqrt 5 + \sqrt {11}$
Show with proof which of these two values is smaller:
$7$, or $\sqrt 2+\sqrt 5 + \sqrt {11}$
I know this problem could be solved using numerous different methods but I am going to post my solution anyway, since I think and I believe I have done a great job in proving it using the most elementary method and the best of observation and thus it earned a place at this blog. :D
$7$, or $\sqrt 2+\sqrt 5 + \sqrt {11}$
I know this problem could be solved using numerous different methods but I am going to post my solution anyway, since I think and I believe I have done a great job in proving it using the most elementary method and the best of observation and thus it earned a place at this blog. :D
One Worked Example of Solving Heuristic IMO Math Problem
Olympiad Algebra Problem:
If $a,\,b,\,x,\,y\in R$ such that
$ax +by =7$
$ax^2+by^2=49$
$ax^3+by^3=133$
$ax^4+by^4=406$
Evaluate $ax^5+by^5$.
The solution from the U.K. mathematician:
If $a,\,b,\,x,\,y\in R$ such that
$ax +by =7$
$ax^2+by^2=49$
$ax^3+by^3=133$
$ax^4+by^4=406$
Evaluate $ax^5+by^5$.
The solution from the U.K. mathematician:
IMO problem that could be solved easily by the linear homogeneous recursion method
Olympiad Algebra Problem:
If $a,\,b,\,x,\,y\in R$ such that
$ax +by =7$
$ax^2+by^2=49$
$ax^3+by^3=133$
$ax^4+by^4=406$
Evaluate $ax^5+by^5$.
If $a,\,b,\,x,\,y\in R$ such that
$ax +by =7$
$ax^2+by^2=49$
$ax^3+by^3=133$
$ax^4+by^4=406$
Evaluate $ax^5+by^5$.
Terence Tao: The World Greatest Mathematician
Some excerpts about the biography and achievement of Terence Tao, or Terry, as he's mostly known, from the major newspapers from the past 9 years:
March 7, 2015
Terence Tao: the Mozart of maths from The Sydney Morning Herald
When he was nine, Tao commenced part-time studies in mathematics at Flinders University. By the time he was 16, he'd finished his science degree. He got his masters when he was 17 and his PhD at Princeton University at 20.
"He is arguably the world's best mathematician," says Joseph Rudnick, the dean of Physical Sciences at the University of California, Los Angeles (UCLA), where Tao, now 39, has been a mathematics professor since he was 24. "Other mathematicians speak of him in tones of awe." His talents, says Rudnick, are "other-worldly".
Tao has pages of awards, fellowships, prizes and medals to his name - most notably, the Fields Medal, the maths world's equivalent of the Nobel Prize, which he received in 2006 when he was 31 "for his contributions to partial differential equations, combinatorics, harmonic analysis and additive number theory". Around about then, people started to describe him as "the Mozart of math".
March 7, 2015
Terence Tao: the Mozart of maths from The Sydney Morning Herald
When he was nine, Tao commenced part-time studies in mathematics at Flinders University. By the time he was 16, he'd finished his science degree. He got his masters when he was 17 and his PhD at Princeton University at 20.
"He is arguably the world's best mathematician," says Joseph Rudnick, the dean of Physical Sciences at the University of California, Los Angeles (UCLA), where Tao, now 39, has been a mathematics professor since he was 24. "Other mathematicians speak of him in tones of awe." His talents, says Rudnick, are "other-worldly".
Tao has pages of awards, fellowships, prizes and medals to his name - most notably, the Fields Medal, the maths world's equivalent of the Nobel Prize, which he received in 2006 when he was 31 "for his contributions to partial differential equations, combinatorics, harmonic analysis and additive number theory". Around about then, people started to describe him as "the Mozart of math".
Mathematical Problem Solving Skill
He first noticed that
$\tan 3(20^\circ)=\tan 60^\circ=\sqrt{3}$
$\tan 3(40^\circ)=\tan 120^\circ=-\sqrt{3}$
$\tan 3(80^\circ)=\tan 240^\circ=\sqrt{3}$
Olympiad Algebra Problem: Evaluate $ax^5+by^5$
Olympiad Algebra Problem:
If $a,\,b,\,x,\,y\in R$ such that
$ax +by =7$
$ax^2+by^2=49$
$ax^3+by^3=133$
$ax^4+by^4=406$
Evaluate $ax^5+by^5$.
If $a,\,b,\,x,\,y\in R$ such that
$ax +by =7$
$ax^2+by^2=49$
$ax^3+by^3=133$
$ax^4+by^4=406$
Evaluate $ax^5+by^5$.
Third Method in Proving $\tan^2 20^{\circ}+\tan^2 40^{\circ}+\tan^2 80^{\circ}=33$
As a good mathematics educator, we should solve the best quality math problems using as many ways as we could, because each solution has its own learning value. Who knows, students might gain something from the long and tedious method of problem solving method and one day, they will surprise us with the improved version of the solution!
One thing every mathematics educator has to remember is that our imaginations are vibrant, our hearts are open, everything about math amazes us, and we think anything is possible.
One thing every mathematics educator has to remember is that our imaginations are vibrant, our hearts are open, everything about math amazes us, and we think anything is possible.
Alternative Way to Prove $\tan^2 x+\tan^2 (x+60^{\circ})+\tan^2 (60^{\circ}-x)=9\tan^2 3x+6$
So in one of my recent post, I mentioned of one rare but extremely useful trigonometry identity that sounds:
$\tan^2 x+\tan^2 (x+60^{\circ})+\tan^2 (60^{\circ}-x)=9\tan^2 3x+6$
We should then use it when appropriate.
$\tan^2 x+\tan^2 (x+60^{\circ})+\tan^2 (60^{\circ}-x)=9\tan^2 3x+6$
We should then use it when appropriate.
Quiz of World Most Famous Mathematician: Terence Tao
Challenging Math Contest Problem: Prove that $\tan^2 x+\tan^2 (x+60^{\circ})+\tan^2 (60^{\circ}-x)=9\tan^2 3x+6$
Given $\tan x+\tan (x+60^{\circ})-\tan (60^{\circ}-x)=3\tan 3x$,
prove that $\tan^2 x+\tan^2 (x+60^{\circ})+\tan^2 (60^{\circ}-x)=9\tan^2 3x+6$.
Wow! This is another exquisite problem that one cannot afford to pass it up but to take it as one tough learning example problem so to train students to be the best. Remember that good teachers will forever encourage learning for understanding and are concerned with developing their students’ critical-thinking skills, problem-solving skills, and problem-approach behaviors. This problem fulfills the these goals of training students to think creatively and that is the reason I bring it to our table.
I won't beat about the bush, so here goes my plan of attack:
prove that $\tan^2 x+\tan^2 (x+60^{\circ})+\tan^2 (60^{\circ}-x)=9\tan^2 3x+6$.
Wow! This is another exquisite problem that one cannot afford to pass it up but to take it as one tough learning example problem so to train students to be the best. Remember that good teachers will forever encourage learning for understanding and are concerned with developing their students’ critical-thinking skills, problem-solving skills, and problem-approach behaviors. This problem fulfills the these goals of training students to think creatively and that is the reason I bring it to our table.
I won't beat about the bush, so here goes my plan of attack:
Olympiad Trigonometry Problem
Prove $\tan^2 20^\circ+\tan^2 40^\circ+\tan^2 80^\circ=33$.
Good trigonometry problem is hard to come by, and when we, the math educator found one, we have to take advantage of it and make full use of it.
Of course, we can rest assured that this trigonometry problem can be tackled using the sum-to-product and product-to-sum identities in a really messy and tedious way. After all, any given math problem can be solved in the most traditional way, isn't it?
Good trigonometry problem is hard to come by, and when we, the math educator found one, we have to take advantage of it and make full use of it.
Of course, we can rest assured that this trigonometry problem can be tackled using the sum-to-product and product-to-sum identities in a really messy and tedious way. After all, any given math problem can be solved in the most traditional way, isn't it?
Exploration of some real life applications of mathematics.
It's high time to launch the campaign to increase awareness of how useful math can be to us, how math helps us in our daily life activities, by us, yes, I mean for just anyone else, a student, a worker, a boss, or a housewife.
But does that mean government has to fork out a handsome sum of money to do that? Not really, in fact, if we could bring in the real scenarios where and when math could be of help in our life, then that alone helps to entice the even most reticent students who always find excuses to hate math, as according to them, math is too big for their brain. If we could show to students some really amazing true stories, that could kindle their passion for math and this doesn't need much money and this has everything to do with if we are capable enough to think of attracting real scenarios and bring them to the classroom.
But does that mean government has to fork out a handsome sum of money to do that? Not really, in fact, if we could bring in the real scenarios where and when math could be of help in our life, then that alone helps to entice the even most reticent students who always find excuses to hate math, as according to them, math is too big for their brain. If we could show to students some really amazing true stories, that could kindle their passion for math and this doesn't need much money and this has everything to do with if we are capable enough to think of attracting real scenarios and bring them to the classroom.
Slideshow 5: Recruit For Attitude, Train For Skills
Math Olympiad Problem: Solve for real solutions
Solve for real solutions for the equation $(2x+1)(3x+1)(5x+1)(30x+1)=10$.
Okay, I heard you, why on earth this problem is supposed to be a delicious question that can promote higher mathematics thinking skills?
One of the most common issues math educators are struggling with is the students who underestimate the so-called trivial math problem and they think by the long and typical tedious solving method, the trivial math problem could be safely and successfully solved without a hitch.
Okay, I heard you, why on earth this problem is supposed to be a delicious question that can promote higher mathematics thinking skills?
One of the most common issues math educators are struggling with is the students who underestimate the so-called trivial math problem and they think by the long and typical tedious solving method, the trivial math problem could be safely and successfully solved without a hitch.
Seeing Pattern Seeing Relationship--- Problem Solving Skill
In my previous post(Heuristic-math-problem-solving-skill), I asked the readers to find the sum of the first $n$ terms for the series:
$1+2(1-x)+3(1-x)(1-2x)+4(1-x)(1-2x)(1-3x)+\cdots+n(1-x)(1-2x)\cdots(1-(n-1)x)$
This is one really hard math Olympiad contest problem, but fortunately logical thinking and heuristic problem solving skills are something that we can teach.
$1+2(1-x)+3(1-x)(1-2x)+4(1-x)(1-2x)(1-3x)+\cdots+n(1-x)(1-2x)\cdots(1-(n-1)x)$
This is one really hard math Olympiad contest problem, but fortunately logical thinking and heuristic problem solving skills are something that we can teach.
Heuristic Math Problem Solving Skill: Seeing Pattern
Brilliant tudents know how and when to implement heuristic strategies. Heuristic strategies are devices which drastically limits the search for a solution in a large problem space (Polya, 2004).
They provide a general suggestion or technique for solving different types of problems and can be used independently or in combination. The ten most common strategies include:
Working backwards, Finding a pattern, Adopting a different point of view, Solving a simpler analogous problem, Considering extreme cases, Making a drawing, Intelligent guessing and testing, Accounting for all possibilities, Organizing data and logical reasoning (Posamentier, Smith and Stepelman, 2006).
They provide a general suggestion or technique for solving different types of problems and can be used independently or in combination. The ten most common strategies include:
Working backwards, Finding a pattern, Adopting a different point of view, Solving a simpler analogous problem, Considering extreme cases, Making a drawing, Intelligent guessing and testing, Accounting for all possibilities, Organizing data and logical reasoning (Posamentier, Smith and Stepelman, 2006).
Intermediate Value Theorem to Prove Inequality Problem
In my previous post, I talked about how to use calculus method to prove that $\sin 10^{\circ} > \dfrac{1}{6}$ (Never Be Complacent).
Or more precisely, the Intermediate Value Theorem as our weapon to prove it.
We will use the triple angle identity for $\sin 3x=3\sin x-4\sin^3 x$ and the value for $\sin 30^{\circ}=\dfrac{1}{2}$ when $x=10^{\circ}$ in our solution:
Or more precisely, the Intermediate Value Theorem as our weapon to prove it.
We will use the triple angle identity for $\sin 3x=3\sin x-4\sin^3 x$ and the value for $\sin 30^{\circ}=\dfrac{1}{2}$ when $x=10^{\circ}$ in our solution:
Never be complacent of your math problem solving skills
Never become complacent with what you have accomplished in the past. Always persuade and inspire your inner self to explore new ideas and venture into new territories so to develop 21st century competencies and become a critical thinker and problem solver.
Small Angle Approximation in Trigonometry
Our previous blog post used the method of proving by contradiction to prove for the inequality $\sin 10^{\circ}>\dfrac{1}{6}$ (Prove that $\sin 10^{\circ}>\dfrac{1}{6}$).
Alternatively, we could also use the "Small-angle Approximation" to prove that $\sin 10^{\circ}>\dfrac{1}{6}$, provided we know fully well that as the angle approaches zero (or the angle is less than $0.2 \,\,\text{radians}$, it is clear that the gap between the approximation and the original function quickly vanishes.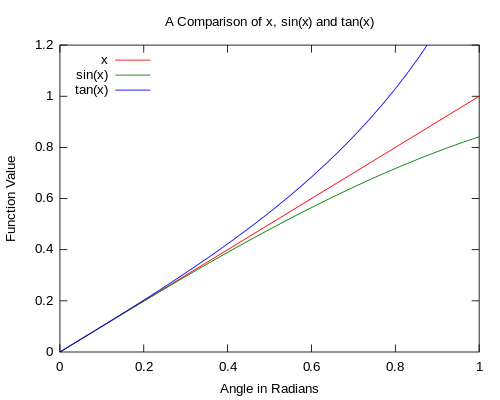
(Graph taken from Small-angle_approximation (Wikipedia))
Alternatively, we could also use the "Small-angle Approximation" to prove that $\sin 10^{\circ}>\dfrac{1}{6}$, provided we know fully well that as the angle approaches zero (or the angle is less than $0.2 \,\,\text{radians}$, it is clear that the gap between the approximation and the original function quickly vanishes.

(Graph taken from Small-angle_approximation (Wikipedia))
Prove that $\sin 10^{\circ}>\dfrac{1}{6}$.
Another heuristic problem solving technique that is so popular and widely use is called "Prove by Contradiction" technique.
Euclid's beautiful proof by contradiction to show there are infinitely many prime numbers is one of the most mind-boggling method to prove something is true that leave us speechless with absolute admiration.
Euclid's beautiful proof by contradiction to show there are infinitely many prime numbers is one of the most mind-boggling method to prove something is true that leave us speechless with absolute admiration.
Show that [MATH]16<\sum_{k=1}^{80}\dfrac{1}{\sqrt{k}}<17[/MATH].
Show that [MATH]16<\sum_{k=1}^{80}\dfrac{1}{\sqrt{k}}<17[/MATH].
On my previous post (Show that [MATH]16<\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\cdots+\dfrac{1}{\sqrt{80}}<17[/MATH]), we used the trapezoid rule to prove the upper bound for the given inequality, i.e. [MATH]16<\sum_{k=1}^{80}\dfrac{1}{\sqrt{k}}[/MATH]. We're then not supposed to use the same method to prove the lower bound simply because the function $y=\dfrac{1}{\sqrt{x}}$ is concave up. No matter how we manipulated that concept, we will only end up with proving the target sum [MATH]\sum_{k=1}^{80}\dfrac{1}{\sqrt{k}}[/MATH] will be greater than some quantity, not less than. This works against to what we are looking to prove, that is, [MATH]\sum_{k=1}^{80}\dfrac{1}{\sqrt{k}}<17[/MATH].
On my previous post (Show that [MATH]16<\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\cdots+\dfrac{1}{\sqrt{80}}<17[/MATH]), we used the trapezoid rule to prove the upper bound for the given inequality, i.e. [MATH]16<\sum_{k=1}^{80}\dfrac{1}{\sqrt{k}}[/MATH]. We're then not supposed to use the same method to prove the lower bound simply because the function $y=\dfrac{1}{\sqrt{x}}$ is concave up. No matter how we manipulated that concept, we will only end up with proving the target sum [MATH]\sum_{k=1}^{80}\dfrac{1}{\sqrt{k}}[/MATH] will be greater than some quantity, not less than. This works against to what we are looking to prove, that is, [MATH]\sum_{k=1}^{80}\dfrac{1}{\sqrt{k}}<17[/MATH].
Prove 16<1/√(1)+1/√(2)+1/√(3)+1/√(4)+...1/√(79)+1/√(80)< 17
Show that [MATH]16 < \sum_{k=1}^{80}\dfrac{1}{\sqrt{k}}< 17[/MATH].
It goes without saying that there's more than one way to skin any given math problem. Exposing students with intriguing math problem can actually instill a genuine interest in creative problem-solving from an early age.
It goes without saying that there's more than one way to skin any given math problem. Exposing students with intriguing math problem can actually instill a genuine interest in creative problem-solving from an early age.
Heuristic Method for Solving Hard System
Solve the system
$\dfrac{1}{x}+\dfrac{1}{y+z}=\dfrac{1}{2}$
$\dfrac{1}{y}+\dfrac{1}{x+z}=\dfrac{1}{3}$
$\dfrac{1}{z}+\dfrac{1}{x+y}=\dfrac{1}{4}$
Method II (Heuristic and satisfactory solution):
$\dfrac{1}{x}+\dfrac{1}{y+z}=\dfrac{1}{2}$
$\dfrac{1}{y}+\dfrac{1}{x+z}=\dfrac{1}{3}$
$\dfrac{1}{z}+\dfrac{1}{x+y}=\dfrac{1}{4}$
Method II (Heuristic and satisfactory solution):
Solving Hard System
Solve the system
$\dfrac{1}{x}+\dfrac{1}{y+z}=\dfrac{1}{2}$
$\dfrac{1}{y}+\dfrac{1}{x+z}=\dfrac{1}{3}$
$\dfrac{1}{z}+\dfrac{1}{x+y}=\dfrac{1}{4}$
Method I (Long and tedious but workable solution):
$\dfrac{1}{x}+\dfrac{1}{y+z}=\dfrac{1}{2}$
$\dfrac{1}{y}+\dfrac{1}{x+z}=\dfrac{1}{3}$
$\dfrac{1}{z}+\dfrac{1}{x+y}=\dfrac{1}{4}$
Method I (Long and tedious but workable solution):
Evaluate ab+bc+ca
Given real numbers $a,\,b,\,c$ such that
$a^2+ab+b^2=2$, $b^2+bc+c^2=3$, $c^2+ca+a^2=5$
Evaluate $ab+bc+ca$.
If nothing that we could do to algebraically manipulate this problem that comes to mind, as this is a hard problem, then what is left for us to be done, is, we can sum the three given equations, to get:
$a^2+ab+b^2=2$, $b^2+bc+c^2=3$, $c^2+ca+a^2=5$
Evaluate $ab+bc+ca$.
If nothing that we could do to algebraically manipulate this problem that comes to mind, as this is a hard problem, then what is left for us to be done, is, we can sum the three given equations, to get:
A Challenge Problem of Simultaneous Equation
Given real numbers $a,\,b,\,c$ such that
$a^2+ab+b^2=2$, $b^2+bc+c^2=3$, $c^2+ca+a^2=5$
Evaluate $ab+bc+ca$.
I hope you would try this problem out and attempt it in every way you could. Break this problem down into smaller cases and solve each piece, experience the process and conquer it!
I will post the suggested solution soon. See you!
$a^2+ab+b^2=2$, $b^2+bc+c^2=3$, $c^2+ca+a^2=5$
Evaluate $ab+bc+ca$.
I hope you would try this problem out and attempt it in every way you could. Break this problem down into smaller cases and solve each piece, experience the process and conquer it!
I will post the suggested solution soon. See you!
Algebraic Method to Tackle the Mock APMO Problem
There exists another way to tackle the previously discussed AMPO mock problem (Asian Pacific Mathematics Olympiad Mock Problem ).
Find [MATH]\sum_{x=0}^{101}\dfrac{\dfrac{2x}{101}-1}{\dfrac{3x^2}{10201}-\dfrac{3x}{101}+1}[/MATH].
In case you are not well prepared to attack the problem analytically, you could still tackle it algebraically, that is purely allowable and no one will ever say algebraic method is not awesome!
For simplicity's sake, we let $x_i=\dfrac{i}{101}$ and $f(x)=\dfrac{\dfrac{2x}{101}-1}{\dfrac{3x^2}{10201}-\dfrac{3x}{101}+1}$, we then have:
Find [MATH]\sum_{x=0}^{101}\dfrac{\dfrac{2x}{101}-1}{\dfrac{3x^2}{10201}-\dfrac{3x}{101}+1}[/MATH].
In case you are not well prepared to attack the problem analytically, you could still tackle it algebraically, that is purely allowable and no one will ever say algebraic method is not awesome!
For simplicity's sake, we let $x_i=\dfrac{i}{101}$ and $f(x)=\dfrac{\dfrac{2x}{101}-1}{\dfrac{3x^2}{10201}-\dfrac{3x}{101}+1}$, we then have:
Asian Pacific Mathematics Olympiad Mock Problem
At first glance, this looks like a very demanding hard challenge, and you don't even know where to start working on the problem.
But this is necessarily a delicious problem in terms of how well we can milk it for all its worth to benefit students. In case you might not already know, I am the advocate for teaching students and equip them with analytical thinking and critical problem solving skills, so, this problem can help me to achieve my aim.
Prove $\tan 55^{\circ}\tan 65^{\circ}\tan 75^{\circ}=\tan85^{\circ}$ (Method II)
$\tan 55^{\circ}\tan 65^{\circ}\tan 75^{\circ}$
$=\tan 55^{\circ}\tan 65^{\circ}\tan 75^{\circ}\cdot \dfrac{\tan85^{\circ}}{\tan85^{\circ}}$
$=\tan85^{\circ}\cdot \dfrac{\tan 55^{\circ}\tan 65^{\circ}\tan 75^{\circ}}{\tan85^{\circ}}$
$=\tan85^{\circ}\cdot \dfrac{\sin 55^{\circ}\sin 65^{\circ}\sin 75^{\circ}(\cos85^{\circ})}{\cos 55^{\circ}\cos 65^{\circ}\cos 75^{\circ}\sin85^{\circ}}$
$=\tan85^{\circ}\cdot \dfrac{(\sin 55^{\circ}\sin 65^{\circ})(\sin 75^{\circ}\cos85^{\circ})}{(\cos 55^{\circ}\cos 65^{\circ})(\cos 75^{\circ}\sin85^{\circ})}$
$=\tan 55^{\circ}\tan 65^{\circ}\tan 75^{\circ}\cdot \dfrac{\tan85^{\circ}}{\tan85^{\circ}}$
$=\tan85^{\circ}\cdot \dfrac{\tan 55^{\circ}\tan 65^{\circ}\tan 75^{\circ}}{\tan85^{\circ}}$
$=\tan85^{\circ}\cdot \dfrac{\sin 55^{\circ}\sin 65^{\circ}\sin 75^{\circ}(\cos85^{\circ})}{\cos 55^{\circ}\cos 65^{\circ}\cos 75^{\circ}\sin85^{\circ}}$
$=\tan85^{\circ}\cdot \dfrac{(\sin 55^{\circ}\sin 65^{\circ})(\sin 75^{\circ}\cos85^{\circ})}{(\cos 55^{\circ}\cos 65^{\circ})(\cos 75^{\circ}\sin85^{\circ})}$
Prove $\tan 55^{\circ}\tan 65^{\circ}\tan 75^{\circ}=\tan85^{\circ}$ (Method I)
Let's begin with the left side:
[MATH]\tan\left(55^{\circ} \right)\tan\left(65^{\circ} \right)\tan\left(75^{\circ} \right)[/MATH]
Using the product to sum identity for the tangent function:
[MATH]\tan(\alpha)\tan(\beta)=\frac{\cos(\alpha-\beta)-\cos(\alpha+\beta)}{\cos(\alpha-\beta)-\cos(\alpha+\beta)}[/MATH]
we may write:
[MATH]\tan\left(65^{\circ} \right)\tan\left(55^{\circ} \right)=\frac{\cos\left(10^{\circ} \right)-\cos\left(120^{\circ} \right)}{\cos\left(10^{\circ} \right)+\cos\left(120^{\circ} \right)}[/MATH]
[MATH]\tan\left(55^{\circ} \right)\tan\left(65^{\circ} \right)\tan\left(75^{\circ} \right)[/MATH]
Using the product to sum identity for the tangent function:
[MATH]\tan(\alpha)\tan(\beta)=\frac{\cos(\alpha-\beta)-\cos(\alpha+\beta)}{\cos(\alpha-\beta)-\cos(\alpha+\beta)}[/MATH]
we may write:
[MATH]\tan\left(65^{\circ} \right)\tan\left(55^{\circ} \right)=\frac{\cos\left(10^{\circ} \right)-\cos\left(120^{\circ} \right)}{\cos\left(10^{\circ} \right)+\cos\left(120^{\circ} \right)}[/MATH]
Calculate $\displaystyle \lim_{x \to \infty} (\sin \sqrt{x+1}-\sin \sqrt{x})$
Calculate $\displaystyle \lim_{x \to \infty} (\sin \sqrt{x+1}-\sin \sqrt{x})$.
Let:
[MATH]L=\lim_{x\to\infty}\left(\sin\left(\sqrt{x+1} \right)-\sin\left(\sqrt{x} \right) \right)[/MATH]
Application of the sum-to-product identity:
Let:
[MATH]L=\lim_{x\to\infty}\left(\sin\left(\sqrt{x+1} \right)-\sin\left(\sqrt{x} \right) \right)[/MATH]
Application of the sum-to-product identity:
Find all the possible values for: $1+a+a^2+\cdots+a^{2011}$
Let $x=a$ be a solution of the equation $x^{2012}-7x+6=0$. Find all the possible values for: $1+a+a^2+\cdots+a^{2011}$.
We're told $x=a$ is a solution of the equation $x^{2012}-7x+6=0$, therefore we have $a^{2012}-7a+6=0$.
It can be rewritten as
$a^{2012}-1-7a+6+1=0$
$a^{2012}-1-7a+7=0$
$(a^{2012}-1)-7(a-1)=0$
We're told $x=a$ is a solution of the equation $x^{2012}-7x+6=0$, therefore we have $a^{2012}-7a+6=0$.
It can be rewritten as
$a^{2012}-1-7a+6+1=0$
$a^{2012}-1-7a+7=0$
$(a^{2012}-1)-7(a-1)=0$
Determine p, q, r, s if p+q+r+s=12, pqrs=27+pq+pr+ps+qr+qs+rs.
This is one very delicious problem that shows how inequality could come into the picture and help in solving system of equations.
Given that $p, q, r, s$ are all positive real numbers and they satisfy the system
$p+q+r+s=12$
$pqrs=27+pq+pr+ps+qr+qs+rs$
Determine $p, q, r$ and $s$.
Okay, our intuition tells us the logic doesn't follow for this problem because we all know very well solving a system of two nonlinear equations in four variables sounds pretty much like a mission impossible.
Given that $p, q, r, s$ are all positive real numbers and they satisfy the system
$p+q+r+s=12$
$pqrs=27+pq+pr+ps+qr+qs+rs$
Determine $p, q, r$ and $s$.
Okay, our intuition tells us the logic doesn't follow for this problem because we all know very well solving a system of two nonlinear equations in four variables sounds pretty much like a mission impossible.
Subscribe to:
Posts (Atom)




























