Prove $\dfrac{\pi}{4}+\dfrac{1}{6}\gt \arctan\left({\dfrac{6}{5}}\right)$.
Do you know if we're pretty familiar with how the graph of a particular function behaves on certain interval, we could set up a definite integral to prove some of the inequality problems (be them hard, moderately hard or very difficult)?
In our case, we know in order to generate the term of $\dfrac{\pi}{4}$ from definite integral, we must have the integral that looks like $\dfrac{1}{x^2+1}$, so it's reasonable if we want to deal with the function of $y=\dfrac{1}{x^2+1}$.
Plotting its graph using the ICT tool that you like, we will see that we have:
Note that the area bounded by $x=1$, $x=\dfrac{6}{5}$, $y=0$ and the curve $y=\dfrac{1}{x^2+1}$ lies completely above the x-axis, that means we will have the result of the definite integral below greater than zero:
[MATH]\begin{align*}\large \int_{1}^{\frac{6}{5}} \dfrac{1}{x^2+1}\,dx&=\left[\arctan x\right]_1^{\frac{6}{5}}\\&=\arctan 1-\arctan \left(\dfrac{6}{5}\right)\\&=\dfrac{\pi}{4}-\arctan \left(\dfrac{6}{5}\right)\gt 0\end{align*}[/MATH]
This yields $\dfrac{\pi}{4}\gt \arctan \left(\dfrac{6}{5}\right)$. Yes, this is a neat result, but this isn't what we're after.
Does this mean we could now ditch this idea of proving the inequality with the integration method?
Nope, this is one approachable and doable method, we should milk this idea for all its worth. But, it's easier said than done, isn't it?
Yes, I have to agree with you to some extent that teachers some of the time expect too much from students. Things could get spirally downwards if teachers don't guide the students all the way through when they are feeding students the enriching (thus challenging) problems.
But this won't be the case between you and me, I would show you how to develop your thinking skills and reasoning skills through working with the intriguing IMO or difficult and challenging math problem.
Back to what we have failed in our first attempt, we have the definite integral:
[MATH]\large \int_{1}^{\frac{6}{5}} \dfrac{1}{x^2+1}\,dx[/MATH] that resulted in $\dfrac{\pi}{4}\gt \arctan \left(\dfrac{6}{5}\right)$.
We could still stick to the integrand, just that we have to add some even functions expressions into it, but keeping in mind we need the resulted area to be bounded by the lines $x=1$, $x=\dfrac{6}{5}$, $y=0$ and the newly defined curve should lie on the first quadrant, so that its area will be a positive.
We know we must introduce some special even function(s) so the graph will remain on the first quadrant on the interval $\left[1,\,\dfrac{6}{5}\right]$.
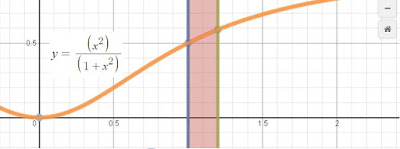
Our first trial would be letting $y= \dfrac{x^2}{x^2+1}$.
When we plot its graph $y= \dfrac{x^2}{x^2+1}$, we see that we're fine, as it lies in the first quadrant and we happily proceed to look for its result, hoping we have our first spot on guess.
[MATH]\begin{align*}\large \int_{1}^{\frac{6}{5}} \dfrac{x^2}{x^2+1}\,dx&=\left[x-\arctan x\right]_1^{\frac{6}{5}}\\&=\left(\dfrac{6}{5}-\arctan \left(\dfrac{6}{5}\right)\right)-\left(1-\dfrac{\pi}{4}\right)\\&=\dfrac{\pi}{4}+\dfrac{1}{5}-\arctan \left(\dfrac{6}{5}\right)\gt 0\end{align*}[/MATH]
i.e. we get:
$\dfrac{\pi}{4}+\dfrac{1}{5}\gt \arctan \left(\dfrac{6}{5}\right)$
But note that $\dfrac{1}{5}\gt \dfrac{1}{6}$ and so we get $\dfrac{\pi}{4}+\dfrac{1}{5}\gt \dfrac{\pi}{4}+\dfrac{1}{6}$.
It's not at all clear to us if $\dfrac{\pi}{4}+\dfrac{1}{6}$ is greater than or less than $\arctan\left({\dfrac{6}{5}}\right)$.
That means the function of $y= \dfrac{x^2}{x^2+1}$ doesn't work.
What if we let $x^2$ be part of the denominator function, like this $y=\dfrac{1}{x^2(x^2+1)}$?
Desmos graphing calculator says its graph lies on the first quadrant for $x\gt 0$.
[MATH]\begin{align*}\large \int_{1}^{\frac{6}{5}} \dfrac{1}{x^2(x^2+1)}\,dx&=\left[-\dfrac{1}{x}-\arctan x\right]_1^{\frac{6}{5}}\\&=\left(-\dfrac{1}{\dfrac{6}{5}}-\arctan \left(\dfrac{6}{5}\right)\right)-\left(-1-\dfrac{\pi}{4}\right)\\&=\dfrac{\pi}{4}+\dfrac{1}{6}-\arctan \left(\dfrac{6}{5}\right)\gt 0\end{align*}[/MATH]
Bingo! It's obvious that we have the right answer now, since we have proved, from the result of the integration that:
$\dfrac{\pi}{4}+\dfrac{1}{6}\gt \arctan \left(\dfrac{6}{5}\right)$ and we're hence done!
See it now? We don't necessarily ditch what we've tried in our first few trials, in fact, they are the perfect guide to developing and refining our previous attempts and we would eventually obtain the most satisfactory and correct answer to the problem at hand.


No comments:
Post a Comment