The given cubic cannot be factored easily and beautifully, so the method of factoring the given polynomial is out of the question.
I hear you, the next best approach might be to try out the substitution method, with the hope that after the substitution, we have less variable terms in our newly set equation. But there seems no suitable substitution is available so to make simpler the given equation.
It's when we feel the pressure. When we get stressed out, the less likely we will be able to solve for the problem at hand.
Ah, ICT could ease the tension that built up within us, as solving for any given equation in International Mathematical Olympiad contest, or even contest within the nation or school should not be something that would stand in our way to rob us of our marks.
We could check with using the appropriate ICT tool the answer for this problem, so we will gain the new perspective on what is really needed to effectively solve for this problem.
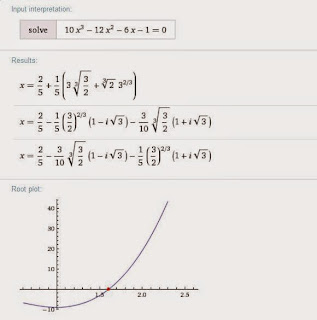
Wolfram alpha is my favorite ICT tool and it tells us solve 10x^3-12x^2-6x-1=0:
$x=\dfrac{2}{5}+\dfrac{1}{5}\left(3\sqrt[3]{\dfrac{3}{2}}+\sqrt[3]{2}(3)^{\frac{2}{3}})\right)$ is the only positive real root.
Looking closely at the "structure" of the exact form of the only positive real root, ah! If we investigate this exact root for a bit, that is, we work backward, we find that:
$\begin{align*}x&=\dfrac{2}{5}+\dfrac{1}{5}\left(3\sqrt[3]{\dfrac{3}{2}}+\sqrt[3]{2}(3)^{\frac{2}{3}})\right)\\&=\dfrac{2}{5}+\dfrac{3(3)^{\frac{1}{3}}}{5(2^{\frac{1}{3}})}+\dfrac{(2)^{\frac{2}{3}}(3)^{\frac{2}{3}}}{5(2^{\frac{1}{3}})}\\&=\dfrac{2(2)^{\frac{1}{3}}}{5(2)^{\frac{1}{3}}}+\dfrac{3(3)^{\frac{1}{3}}}{5(2^{\frac{1}{3}})}+\dfrac{(2)^{\frac{2}{3}}(3)^{\frac{2}{3}}}{5(2^{\frac{1}{3}})}\\&=\dfrac{(2)^{\frac{4}{3}}+(2)^{\frac{2}{3}}(3)^{\frac{2}{3}}+(3)^{\frac{4}{3}}}{5(2^{\frac{1}{3}})}---(*)\end{align*}$
Recall that if we multiply $a^2+ab+b^2$ by $a-b$, it yields:
[MATH]\color{yellow}\bbox[5px,purple]{(a-b)(a^2+ab+b^2)=a^3-b^3}[/MATH]
From the expression of the numerator at (*), we see that we have:
$\begin{align*}(2)^{\frac{4}{3}}+(2)^{\frac{2}{3}}(3)^{\frac{2}{3}}+(3)^{\frac{4}{3}}&=((2)^{\frac{2}{3}})^2+(2)^{\frac{2}{3}}(3)^{\frac{2}{3}}+((3)^{\frac{2}{3}})^2\\&=a^2\,\,\,\,\,\,\,\,\,\,\,\,+ab\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+b^2\end{align*}$
with $a=(2)^{\frac{2}{3}}$ and $b=(3)^{\frac{2}{3}}$.
Therefore, we could simplify $(2)^{\frac{4}{3}}+(2)^{\frac{2}{3}}(3)^{\frac{2}{3}}+(3)^{\frac{4}{3}}$ in the following manner:
[MATH]\color{yellow}\bbox[5px,purple]{(a-b)(a^2+ab+b^2)=a^3-b^3}[/MATH]
$\begin{align*}((2)^{\frac{2}{3}}-(3)^{\frac{2}{3}})(((2)^{\frac{2}{3}})^2+(2)^{\frac{2}{3}}(3)^{\frac{2}{3}}+((3)^{\frac{2}{3}})^2)&=((2)^{\frac{2}{3}})^3-((3)^{\frac{2}{3}})^3\\&=2^2-3^2\\&=4-9\\&=-5\end{align*}$
Picking up where we left off at (*) by multiplying the top and bottom of the fraction by the quantity [MATH]\color{yellow}\bbox[5px,blue]{(2)^{\frac{2}{3}}-(3)^{\frac{2}{3}}}[/MATH], we have:
[MATH]\begin{align*}x&=\dfrac{(2)^{\frac{4}{3}}+(2)^{\frac{2}{3}}(3)^{\frac{2}{3}}+(3)^{\frac{4}{3}}}{5(2^{\frac{1}{3}})}\\&=\dfrac{((2)^{\frac{4}{3}}+(2)^{\frac{2}{3}}(3)^{\frac{2}{3}}+(3)^{\frac{4}{3}})}{(5(2^{\frac{1}{3}}))}\dfrac{\cdot (\, \color{yellow}\bbox[5px,blue]{(2)^{\frac{2}{3}}-(3)^{\frac{2}{3}}}\,\color{black}{)}}{\cdot (\, \color{yellow}\bbox[5px,blue]{(2)^{\frac{2}{3}}-(3)^{\frac{2}{3}}}\,\color{black}{)}}\\&=\dfrac{-5}{5((2)^{\frac{1}{3}}(2)^{\frac{2}{3}}-(2)^{\frac{1}{3}}(3)^{\frac{2}{3}})}\\&=\dfrac{-\cancel{5}}{\cancel{5}((2)^{\frac{1}{3}}(2)^{\frac{2}{3}}-(2)^{\frac{1}{3}}(3)^{\frac{2}{3}})}\\&=\dfrac{1}{(2\cdot 3^2)^{\frac{1}{3}}-2}\\&=\dfrac{1}{18^{\frac{1}{3}}-2}\end{align*}[/MATH]
Things are all fallen in place and we're definitely on the right track now. If we keep on going, we see the more promising result:
From
$x=\dfrac{1}{18^{\frac{1}{3}}-2}$
We could algebraically manipulate it to get the perfect and right idea on how to approach this problem successfully.
$\dfrac{1}{x}=18^{\frac{1}{3}}-2$
$\dfrac{1}{x}+2=18^{\frac{1}{3}}$
$\dfrac{1+2x}{x}=18^{\frac{1}{3}}$
$\left(\dfrac{1+2x}{x}\right)^3=18$
$(1+2x)^3=18x^3$
$1+3(2x)+3(2x)^2+(2x)^3=18x^3$
$1+6x+12x^2+8x^3=18x^3$
Ah! Can you see it now?
The surest way to approach the problem is to first recognize that $(1+2x)^3=1+6x+12x^2+8x^3$ and since we're given $10x^3-12x^2-6x-1=0$, we could replace $10x^3=12x^2+6x+1$ into $(1+2x)^3=1+6x+12x^2+8x^3$ to get
$(1+2x)^3=10x^3+8x^3$
Of course we would do this on another draft paper, so, in the real exam, we would act like we recognize the pattern at an instant and get started to work with $(1+2x)^3=1+6x+12x^2+8x^3$ instead, hehehe...
Therefore, working backward with the help of appropriate ICT tool are two important weapons that we have to help us to become a lateral thinker.
In this lesson, we learn that working backwards is a really powerful tool when it can be used. It frequently turns out to be worth looking at what happens at the end and then work backward to the beginning, in order to see what move(s) is/are best.
K.M. Weiland once said:
When you can work your way backwards from a known plot point, finding your way becomes as simple as filling in the blanks.

No comments:
Post a Comment