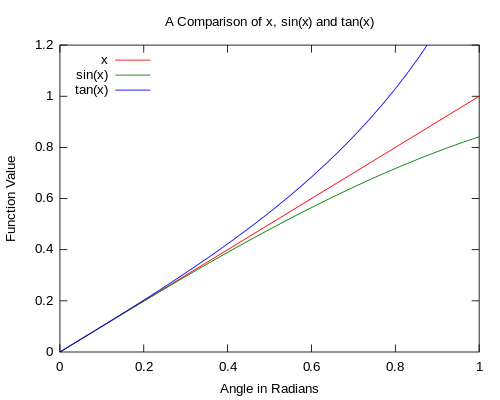
Alternatively, we could also use the "Small-angle Approximation" to prove that $\sin 10^{\circ}>\dfrac{1}{6}$, provided we know fully well that as the angle approaches zero (or the angle is less than $0.2 \,\,\text{radians}$, it is clear that the gap between the approximation and the original function quickly vanishes.
(Graph taken from Small-angle_approximation (Wikipedia))
Our target expression, i.e. $10^{\circ}$ is equivalent to $\dfrac{10^{\circ}\pi}{180^{\circ}}$.
Since $\pi=3.14159265\cdots > 3$, we have:
$\dfrac{10^{\circ}\pi}{180^{\circ}}> \dfrac{10^{\circ}(3)}{180^{\circ}}=\dfrac{1}{6}$
Small-angle Approximation tells us when the angle is sufficiently small, then we have:
$\sin x \approx x$
And this directly proves that $\sin 10^{\circ}=\sin \dfrac{10^{\circ}\pi}{180^{\circ}} \approx \dfrac{10^{\circ}\pi}{180^{\circ}} >\dfrac{1}{6}$
and we're done.
For some passive students, when they are provided the graph of comparison between $x,\,\sin x$, they only blindly receive and accept that when $x$ is sufficiently small, then we could use the approximation $\sin x \approx x$ to estimate the value for $\sin x$.
They don't care what else they could glean from the graph. But, for some bright students, they would examine the graph clearly and in detail so they know when we have to find the value for $\sin 6^{\circ}$, we can adopt the small angle approximation principle to prove that $\sin 6^{\circ}>\dfrac{1}{6}$ in merely a few steps and the result is powerful and convincing.
Therefore, math educators should end this practice by encouraging students to generate some rich and useful observations from the given graph by orally testing their full understanding to what past mathematicians had proved for us, or to give them impromptu quizzes to keep them on their toes.
No comments:
Post a Comment